Логическими переменными

Одна и та же задача может решаться аналоговыми или цифровыми методами.

Цифровые устройства, решающие задачу аналогичную с аналоговыми устройствами, содержат гораздо большее число элементов. Вместо одной линии обработки информации требуется N линий.

Цифровые устройства кажутся относительно сложными, однако они основаны на принципе многократного повторения относительно простых базовых логических схем. Связи между этими схемами строятся на основе чисто формальных методов. Даже самые сложные преобразования цифровой информации, в конечном счете, сводятся к простейшим операциям над сигналами 0 и 1.

Инструментом такого построения служит булева алгебра, которая называется также алгеброй логики.

В отличие от переменной в обычной алгебре логическая переменная в булевой алгебре имеет только два значения – "истинность" и "ложность", которые называются логическим нулем и логической единицей. В качестве обозначений используются "1" и "0".

Существуют три основные (базовые) операции между логическими переменными:

1. конъюнкция (логическое умножение), иначе операция И.

2. дизъюнкция (логическое сложение), иначе операция ИЛИ;

3. инверсия (логическое отрицание), иначе операция НЕ.

Введем условные обозначения:

· F - значение выходного сигнала:

· Х1 и Х2 - значения входных сигналов.

Тогда базовые логические операции можно записать в виде представленном в Таблице 1.1.

Таблица 1.1

Операция	Логическое выражение	Определение
Конъюнкция	F = Х1*Х2 = Х1 L Х2	Значение функции И истинно (равно 1) тогда и только тогда, когда все её аргументы (Х1 и Х2) равны 1, т.е. истинны.
Дизъюнкция	F = Х1+Х2 = Х1 Ú Х2	Значение функции ИЛИ истинно (равно 1) тогда, когда хотя бы один из ее аргументов (Х1 или Х2, или Х1 и Х2) равны 1, т.е. истинны.
Инверсия	___ F = Х1	Значение F истинно тогда, когда аргумент (Х1) является ложным

Применительно к логическим операциям существуют теоремы, приведенные в Таблице 1.2.

Таблица 1.2

Наименование	Для умножения	Для сложения
Коммутативный закон	Х₁Х₂ = Х₂Х₁	Х₁₊Х₂ = Х₂₊Х₁
Ассоциативный закон	Х₁(Х₂Х₃) = (Х₁Х₂)Х₃	Х₁₊(Х₂₊Х₃) = (Х₁₊Х₂)+Х₃
Дистрибутивный закон	Х1(Х2 + Х3) = Х1Х2+ Х1Х3
Правило повторения	ХХ = Х	Х+Х=Х
Правило отрицания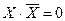
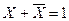
Правило двойного отрицания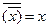
Теорема де Моргана: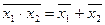
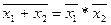
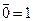
Операции с 0 и 1:	Х×1=1 Х×0=0	Х+1=1 Х+0=Х

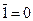
Многие из этих теорем известны из алгебры чисел. Однако некоторые теоремы для чисел несправедливы; кроме того, понятие "инверсия" (отрицание) для чисел вообще не определено.

С помощью выражений алгебры логики можно вычислить результаты логических операций для всех возможных значений входных переменных и определить их таблицы истинности.

<1 234 5 6 7 >

Дата добавления: 2021-12-14; просмотров: 298;