Дифференциальные уравнения с разделяющимися переменными.
Дифференциальные уравнения вида
f(x)dy = g(y)dx
нельзя сразу решить интегрированием, так как левая и правая его части имеют две независимые переменные, а для интегрирования необходимо, чтобы каждая переменная находилась в той части уравнения, в которой находится ее диференциал.
Дифференциальные уравнения, в которых переменные можно разделить, если умножить обе части уравнения на одно и то же выражение, называются дифференциальными уравнениями с разделяющимися переменными.
Нужно помнить, что при делении обеих частей уравнения на функцию, можно потерять некоторые решения.
Чаще всего общее решение дифференциального уравнения получаем в неявном виде и нет особой нужды решать его относительно одной из переменных, так как в дифференциальном уравнении независимые переменные считаются равноправными.
Например: решить дифференциальное уравнение:
 ,
,
Разделим переменные и получим
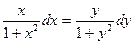 , проинтегрировав обе части, получим:
, проинтегрировав обе части, получим:
 , пропотенцировав, получим общее решение данного дифференциального уравнения:
, пропотенцировав, получим общее решение данного дифференциального уравнения:
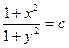 .
.
Дата добавления: 2020-11-18; просмотров: 404;











