Упрощение и минимизация логических функций
Сложность логической функции, а отсюда сложность и стоимость реализующей ее схемы, пропорциональны числу операций и числу вхождений перемещений или их отрицаний.
Логическая функция может быть упрощена с помощью аксиом и теорем алгебры логики, однако такие преобразования требуют громоздких выкладок и навыков.
На практике для упрощения логических выражений описывающих работу устройства применяют Карты Карно
Рассмотрим булево выражение:
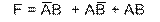
Для реализации данного выражения необходимо 2 инвертора, 3 конъюнктора (И) и 1 дизъюнктор (ИЛИ).
Упростим данное логическое выражение
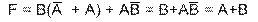
Таким образом, все логическое выражение сведено к логической операции ИЛИ (конъюнктор).
Карта Карно представляет собой графическое изображение всех возможных наборов значений аргументов, каждый минтерм изображается на карте виде клетки.
Карта образуется путем такого расположения клеток при котором минтермы, находящиеся в соседних клетках, отличаются значением одной переменной.
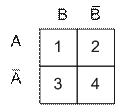
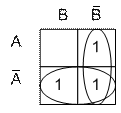
Карты Карно для 2 переменных имеет вид, представленный на Рис.1.10.а.
Минимизируем исходное логическое выражение посредством применения карт Карно.
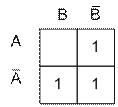
Проставим 1 в карту Карно в те клетки, которые соответствуют наборам функции присутствующим в логическом выражении.
Отыскание минимальной формы сводится к максимальному склеиванию по некоторому аргументу – по В – вертикаль и по А – горизонталь.
Соседние 1 объединим контуром (Рис.1.10.в. ). Возможно объединение 2, 4, 8 и т.д. единиц, стоящих в соседних клетках, кроме этого карта карно может быть свернута в горизонтальный или вертикальный цилиндры, или шар, что также позволяет объединить 1 стоящие в соседних крайних клетках свернутых карт.
Т.к. у нас два контура, то новое выражение будет состоять из двух членов связанных функцией ИЛИ.
| 
| 
|
| а) | б) | с) |
| Рис.1.10. Упрощение логического выражения с помощью карты Карно |
Для нижнего контура аргумент А встречается с 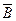 и В, но в соответствии с правилом булевой алгебры аргументы
и В, но в соответствии с правилом булевой алгебры аргументы 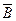 и В дополняют друг друга и их можно опустить, т.е.остается только аргумент А.
и В дополняют друг друга и их можно опустить, т.е.остается только аргумент А.
В результате значение функции будет также сведено к логической операции ИЛИ.
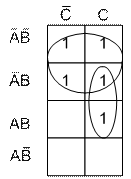
Рассмотрим пример построения карты Карно на три переменные. Пусть дано логическое выражение
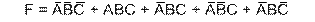
Карта Карно и результат минимизации представлены на Рис.1.11.
|
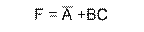
|
| Рис.1.10. Пример карты Карно для 3-х переменных |
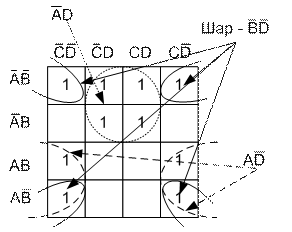
Рассмотрим пример построения карты Карно на четыре переменные (Рис.1.11)/
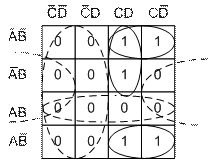
В рассмотренных примерах осуществлялась минимизация по 1, однако в некоторых случаях более удобной может оказаться минимизация по 0. Пример такого случая представлен на Рис.1.12.
Минимизация по нулям показана штрихпунктирной линией, а по единицам – сплошной.
При минимизации по нулям получается отрицательная функция. Поставив отрицание с двух сторон.
|
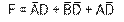
|
| Рис.1.11. Карта карно на 4 переменных. |
| Минимизация по 0
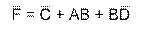
|
Минимизация по 1
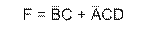
| |
| Рис.1.12. Минимизация по 0 |
Используя теорему Де-Моргана можно перейти к положительной функции и реализовать полученное значение на требуемых логических элементах.
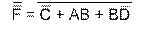
|
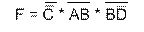
|
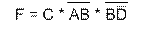
|
Дата добавления: 2021-12-14; просмотров: 562;











