Числа, используемые в цифровой электронике

<1 2 345 6 7 >

Возможность применения булевой алгебры для решения задач анализа и синтеза цифровых устройств обусловлена аналогией понятий и категорий этой алгебры и двоичной системы счисления, которая положена в основу представления преобразуемых устройством сигналов.

Двоичная система счисления – это система с основанием 2 (2 цифры: 0 и 1). Относится к позиционной системе счисления (в зависимости от расположения цифры в числе цифра имеет разный вес).

Символы десятичной системы соответствуют символам двоичной системы счисления:

0 = >0; 1 => 1; 2 => 10; 3 => 11; 4 => 100; 5 => 101; 6 => 110; 7 => 111; 8 => 1000; 9 => 1001

Двоичное число можно преобразовать в десятичное число используя соответствующий вес разряда двоичного числа.

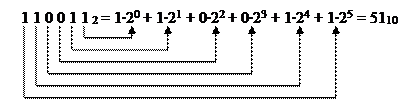
Обратное преобразование (из десятичного числа в двоичное) выполняется путем деления каждого промежуточного частного на 2. При этом каждый неделимый конечный остаток дает очередную цифру для искомого двоичного числа. Деление происходит до тех пор, пока частное не будет равно 0.

Двоичное число представляет собой полученные остатки, записанные в порядке от последнего к первому, как показано на примере.

13 : 2 = 6 1 1 Остаток 1

6 : 2 = 3 0 2 =>1101₂ Остаток 0

3 : 2 = 1 1 4 Остаток 1

1 : 2 = 0 1 8 Остаток 1

В цифровых устройствах используется также шестнадцатеричная система счисления. Она является вспомогательной и используется при подготовке задач к решению.

За основание шестнадцатеричной системы принято число 16. Она является избыточной по отношению к 10 системе. Помимо цифр от 0 до 9 в шестнадцатеричной системе счисления используются буквы А(10), B(11), C(12), D(13), E(14), F(15). Каждая цифра или буква кодируется четырьмя двоичными разрядами.

Цифровые устройства должны иметь возможность обрабатывать как положительные, так и отрицательные двоичные числа.

Для работы с отрицательными или положительными цифрами используется так называемый знаковый разряд (старший разряд).

Положительное число кодируется 0 в знаковом разряде ([0]0010₂).

Перевод из двоичной системы в шестнадцатеричную систему	Перевод из шестнадцатеричной системы в двоичную систему
	2F₁₆ => 00101111 => 101111₂

Отрицательное число - 1.

Для упрощения выполнения операций над отрицательными двоичными числами используются коды, приведенные в таблице 1.3.

Дополнительный код иначе называют дополнением до 2 или полным

Пример: [X]_пр= [0]1001₂ = 1*2⁰+0*2¹+0*2²+0*2³+0*2⁴=1+8=9₁₀

[X]_обр = [1]0110₂ = 0*2⁰+1*2¹+1*2²+0*2³–1*2⁴=2+4-16= – 10₁₀

[X]_доп = [1]0111₂ = 1*2⁰+1*2¹+1*2²+0*2³-1*2⁴=1+2+4-16= – 9₁₀

Таблица 1.3

Наименование	Значение	Пояснения
Прямой код [Х]_пр	[X]_пр = [1]00101
Обратный код [Х]_обр	[X]_обр = [1]11010	Обратный код отрицательного числа формируется по следующему принципу: в знаковый разряд заносится 1, а все остальные разряды меняются на обратные по отношению к прямому коду этого числа
Дополнительный код [Х]_доп	[X]_доп = 1]11011	Дополнительный код отрицательного числа формируется по следующему принципу: младший разряд обратного кода складывается с 1.