Дифференциальные уравнения первого порядка с разделяющимися переменными.

Если дифференциальное уравнение может быть представлено в виде Р(x)dx = Q(t)dt, где функция Р(x) зависит только от x, а функция Q(t) зависит только от t, то говорят, что переменные разделяются. В этом случае имеем

.

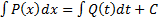Пример 1. Точка движется прямолинейно со скоростью V = gt (V в м/c, t в c). Найти закон ее движения, если при t = 0 x₀ = 1 м.

Решение. Так как

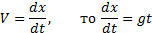
и движение точки описывается дифференциальным уравнением с разделяющимися переменными: dx = gtdt.В результате интегрирования получаем: x = gt²/2 + C. Подставив в это уравнение начальное условие x₀ = 1 м при t = 0, получим: С = 1 м. Следовательно, закон движения точки имеет вид: x = (gt²/2 + 1) м.

Пример 2. Точка движется прямолинейно со скоростью V = 5x (м/c). Найти закон движения точки, если при t = 0 x₀ = e (м).

Решение. Так как

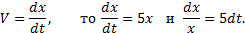
В результате интегрирования получаем: ln x = 5t + C. Используя начальные данные, находим постоянную: С = ln e = 1 м. Следовательно, закон движения точки имеет вид x = e^5t+1 (м).

II. Контрольные вопросы:

1. Какое уравнение называется дифференциальным?

2. Что называется порядком дифференциального уравнения?

3. Что называется решением дифференциального уравнения?

4. Какое решение дифференциального уравнения называется общим и какое – частным?

5. Сформулируйте задачу Коши.