Кардинальные числа : арифметика

Прежде всего, заметим, что если A, B Í U, то можно найти такие множества A¢, B¢ Í U, что A ~ A¢, B ~ B¢, A¢ Ç B¢ = Æ. Действительно, достаточно положить A¢ = {u₁}´A, B¢ = {u₂}´B , где u₁ , u₂ Î U, u₁ ¹ u₂ . Ясно, что соответствия a ® (u₁ ; a) (a Î A) и b ® (u₁ ; b) (b Î B) между множествами A и A¢ , B и B¢ биективны и A¢ Ç B¢ = Æ (?!).

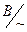Сумма + : Пусть a = , b = Î Card(U). Тогда их суммой называется кардинал g = .

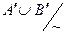Это определение не зависит от конкретных представителей A и B: если a = 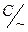, b = 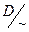, то С ~ A, D ~ B, так что C¢ ~ A¢, D¢ ~ B¢ и C¢ È D¢ ~ A¢ È B¢. Поэтому 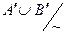= g = .

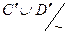Аналогично можно определить и суммыобщего вида: если есть множество кардиналов {a_i = 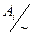| i Î I }, то по множествам A_i построим непересекающиеся попарно множества A¢_i = {{i}}´A_i Í U (?!) и суммой 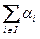назовём кардинал 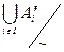, который тоже не зависит от представителей A_i (i Î I).

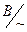Произведение × :Пусть a = , b = Î Card(U). Тогда их произведением a×b называется кардинал g = . Аналогично, в общем случае, если есть множество кардиналов {a_i = 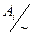| i Î I }, то произведением 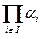назовём кардинал 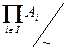. Убедитесь, что эти определения не зависят от представителей.

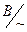Степень : Пусть a = , b = Î Card(U). Тогда степенью a ^b называют кардинал a ^b = 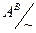, где, как обычно, A^B – множество всех отображений из B в A: A^B = {f : B ® A | f – отображение}.