Порядок на кардиналах

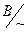Используемое выше словосочетание “промежуточный кардинал” предполагает, конечно, упорядочивание кардиналов. Порядок вводится естественным образом: если a = , b = – два кардинала, то, как известно, может выполняться одно из трёх условий |A| < |B|, |A| = |B|, |A| > |B|, в соответствии с которыми полагают a < b, a = b, a > b . Ясно, что это определение не зависит от выбора представителей: если a = 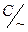, b = 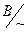, то по определению классов эквивалентности, C ~ A, D ~ B, т.е. |C| = |A|, |D| = |B|, и отношение порядка между |C| и |D| будет таким же, как между |A| и |B|.

Легко понять, что введённое бинарное отношение на множестве Card(U) действительно является отношением линейного порядка, т.е.

рефлексивно: (" a Î Card(U) a £ a),

транзитивно:(" a , b , g Î Card(U) (a £ b) Ù (b £ g) ® (a £ g)),

антисимметрично: ((" a , b Î Card(U) (a £ b) Ù (b £ a) ® (a = b)),

линейность: (" a , b Î Card(U) (a < b) Ú (a = b) Ú (a > b)).

Это сразу следует из доказанных выше соответствующих свойств для мощностей множеств.

Оказывается, что порядок на кардиналах является полным, т.е. любое множество кардиналов содержит наименьший элемент. Для этого используется аксиома выбора в форме теоремы Цермелло (глава I, § 7, теорема об эквивалентных формулировках аксиомы выбора). Таким образом, каждый a = кардинал можно считать связанным с в.у.м. (A £ ).

Если (A < ), (B, p ) – два л.у.м., то назовём A начальным отрезком B, если существует инъекция t : A ® B со свойствами:

" b Î B (b Î t(A)) Ú (" x Î A t(x) p b), " x, y Î A (x < y) « (t(x) p t(y)).

Первое условие означает, что множество t(A) не имеет предшественников в B, а второе – что отображение t сохраняет порядок.

Если t биективно, то множества A и B назовём подобными.

Лемма (трихотомия вполне упорядоченных множеств). Для любых вполне упорядоченных множеств (A, < ) и (B, p ) реализуется ровно одна из трёх возможностей: A – начальный отрезок B, A подобно B, B – начальный отрезок A.

Доказательство.Начнём строить отображение t : A ® B, сохраняющее порядок. Выберем во множествах A и B наименьшие элементы a и b соответственно и положим t(a) = b. Таким образом, задано отображение начальных отрезков t : {a} ® {b}. Пусть отображение t : O_A ® O_B уже построено для начальных отрезков O_A Í A, O_B Í B. Если O_A = A, то A – начальный отрезок B. Если O_B = B, то отображение t ^–1 : B ® O_A даёт основание утверждать, что B – начальный отрезок A. Если же A \ O_A ¹ Æ ¹ B \ O_B , то в этих множествах есть наименьшие элементы u и v, так, что можно расширить отображение t : O_A È {u} ® O_B È {v}, полагая t(u) = v. Ясно, что t сохраняет порядок и отображает начальный отрезок множества A на начальный отрезок множества B.

Таким образом, либо будет постоено искомое вложение t : A ® O_B Ì B, либо вложение t ^–1 : B ® O_A Ì A, либо биекция t : A ® B.

Лемма доказана.

Замечание: Проведённое доказательство не вполне строго, хотя и адекватно отражает суть дела. Нужно рассматривать тройки (t , D(t), Im(t)), введя на них частичный порядок (большая тройка как функция продолжает меньшую), доказать, что у каждой возрастающей цепи троек есть верхняя грань, и воспользовавшись леммой Цорна, найти максимальный элемент, который будет иметь один из трёх видов (t , A, O_B), (t , O_A , B), (t , A , B). Подобные рассуждения проведены в доказательстве теоремы об эквивалентных формулировках аксиомы выбора (глава I, § 7).

Теорема (о полном порядке на множестве кардинальных чисел). Введённый линейный порядок на множестве Card(U) кардинальных чисел универсума U является полным, т.е. любое его непустое подмножество имеет наименьший элемент.

Доказательство. Воспользуемся леммой:

Лемма (критерий полной упорядоченности). Линейно упорядоченное множество (А, £) вполне упорядочено отношением £ тогда и только тогда, когда не существует бесконечной строго убывающей цепочки

а₁ > а₂ > … > а_n > …

Доказательство. (Þ) Пусть вначале л.у.м. (А, £) вполне упорядочено, т.е. каждое его непустое подмножество имеет наименьший элемент. Это сразу показывает, что в А не может быть бесконечной строго убывающей цепочки а₁ > а₂ > … > а_n > … , т.к. во множестве {a₁ , a₂ , … , a_n , … } нет наименьшего элемента.

(Ü) Обратно, пусть в А нет бесконечных строго убывающих цепочек а₁ > > а₂ > … > а_n > … . Докажем, что каждое непустое подмножество в А имеет наименьший элемент. Если в Æ ¹ M Í A нет наименьшего элемента, то выберем произвольный элемент m₁ Î M . Поскольку онне наименьший, то найдётся m₂ < m₁ . Продолжая этот процесси пользуясь аксиомой выбора (?!), построим цепочку m₁ > m₂ > … > m_n > … – противоречие.

Лемма доказана.

Применим доказанный критерий к л.у.м. (Card(U), £ ). Предположим, что существует цепь кардиналов a₁ > a₂ > … > a_n > … . При этом каждое множество a_i (i Î N) можно считать в.у.м. По лемме о трихотомии для в.у.м. для любых соседних кардиналов a_i , a_i+1 выполнено одно из двух (?!): либо a_i – собственный отрезок a_i+1 , либо a_i+1 – собственный отрезок a_i . Ввиду определения порядка > , получаем |a_i+1| < |a_i| , а значит, a_i не может быть собственным отрезком a_i+1 (?!). Значит, a_i+1 – собственный отрезок a_i , и можно считать, что a_i+1 Ì a_i (отождествляя элемент x Î a_i+1 с элементом t(x) Î a_i при отображении t : a_i+1 ® a_i ). Таким образом, все множества a₂ , a₃ , … , a_n , … – начальные отрезки в в.у.м. a₁ . Выберем, пользуясь аксиомой выбора, элементы m_i Î a_i \ a_i+1 (i Î N). Тогда m₁ f m₂ f … f m_n f … – бесконечная убывающая цепь в в.у.м. (a₁ , f ) – противоречие.

Теорема доказана.