Основные свойства операций с кардиналами

1⁰. " a , b , g, d Î Сard(U) a £ b Ù g £ d ® a + g £ b + d

Пусть кардиналы a , b , g, d соответствуют попарно непересекающимся множествам A, B, C, D. Нужно доказать, что если существуют инъекции f : A ® B и j : C ® D, то существует инъекция h : A È C ® B È D. Зададим h(x) = 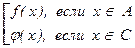. Это – инъекция, т.к. если h(x) = h(y), то x и y не могут принадлежать разным множествам (А Ç С = Æ), и значит, выполнены равенства f(x) = f(y) или j(x) = j(y), откуда (ввиду инъективности отображений f и j) x = y.

2⁰. " a , b , g, d Î Сard(U) a £ b Ù g £ d ® a×g £ b×d

Аналогично предыдущему. Пусть кардиналы a , b , g, d соответствуют попарно непересекающимся множествам A, B, C, D. Нужно доказать, что если существуют инъекции f : A ® B и j : C ® D, то существует инъекция h : A´C ® B´D. Зададим h((a; c)) = (f(a) ; j(c)) . Проверьте сами, что это – инъекция.

3⁰. " a , b , g Î Сard(U) (a + b) + g = a + (b + g)

Нужно доказать, что для попарно непересекающихся множеств A, B, C верно |(A È B) È C| = |A È (B È C)|. Это очевидно ввиду закона ассоциативности объединения.

4⁰. " a , b Î Сard(U) a + b = b + a

Аналогично предыдущему.

5⁰. $ 0 Î Сard(U) " a Î Card(U) 0 + a = a = a + 0

6⁰. " a , b , g Î Сard(U) (a×b)×g = a×(b×g)

Нужно доказать, что |(A´B)´C| = |A´(B´C)|. Биекция между этими множествами естественна: ((a; b); c) « (a; (b; c)).

7⁰. " a , b Î Сard(U) a×b = b×a

Самостоятельно.

8⁰. $ 1 Î Сard(U) " a Î Card(U) 1×a = a = a×1

9⁰. " a , b , g Î Сard(U) (a + b)×g = a×g + b×g

Нужно доказать, что |(A È B)´C| = |(A´C) È (B´C)| для непересекающихся A, B. Это следует из (A È B)´C = (A´C) È (B´C).

10⁰. " a , b , g Î Сard(U) a ^{b + g} = a ^b×a ^g

Нужно доказать, что |A^{B È C}| = |A^B´A^C| для непересекающихся B и C. Биекция естественна: отображению f : B È C ® A ставим в соответствие пару функций (f |_B ; f |_C) Î A^B´A^C, где f |_X – ограничение функции f на множество X Í B È C.

11⁰. " a , b , g Î Сard(U) (a×b)^g = a ^g×b ^g

Равенство |(A´B)^C| = |A^C´B^C| проверяется построением биекции, ставящей в соответствие функции f : C ® A´B пару функций (f_A ; f_B), где f_A = π_Aof, f_B = π_Bof (π_A и π_B – естественные проекции множества A´B на сомножители).

12⁰. " a , b Î Сard(U) (a ^b)^g = a^(b×g)

Равенство |(A^B)^C| = |A^B´C| проверяется построением биекции, ставящей в соответствие отображению f : C ® A^B отображение g : B´C ® A где g((b; c)) = f(c)(b) Î A (нужно помнить, что f(c) Î A^B является отображением из B в А).

13⁰. 1 + 1 + … = w, k₁ + k₂ + … = w

|{a₁} È {a₂} È …| = |{a₁ , a₂ , …}| = |N| при попарно различных a_i (i Î N),

|{1, … , k₁} È {k₁ + 1, … , k₁ + k₂ + 2} È …| = |N|.

14⁰. w + w + … = w

Объединение счётного числа счётных множеств счётно.

15⁰. n×w = w = w ⁿ

Декартово произведение конечного числа счётных множеств счётно, а значит, n×w = w. Кроме того, w ⁿ = 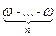= w ²×w ^n–2 = w×w ^n–2 = w ^n–1 = … = w.

16⁰. 1+ w + w ² + … + w ⁿ + … = w

Объединение счётного числа счётных множеств счётно.

17⁰.n^w = w ^w = c^w = c = 2^w = w×с

Прежде всего, c = |[0; 1]| = |{0, c₁c₂ … Î R | c_i – двоичные цифры}|. Поэтому c – мощность всех последовательностей с компонентами из двухэлементного множества цифр, т.е. c = 2^w.

Далее, с = 2^w £ n^w £ w ^w £ c ^w = (2 ^w)^w = 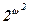= 2 ^w = c, так что все эти мощности равны.

Наконец, c £ w×c £ c ² = c .

18⁰. 1+ с + с ² + … + с ⁿ + … = 1+ с + с + … + с + … = w×с = с

19⁰. " a , b Î Сard(U) (a ³ w Ú b ³ w) ® (a×b = max{a, b})

Достаточно доказать для бесконечного кардинала a равенство a ² = a : если a ³ b , то a £ a×b £ a ² = a , и значит, a×b = a = max{a, b}.

Пусть для некоторого бесконечного кардинала a верно a ² ¹ a. Тогда во в.у.м. Card(U) можно выбрать наименьший кардинал с этим свойством, который и обозначим через a. По выбору a имеем " b < a b ² = b. Рассмотрим произвольный отрезок w £ b < a и рассмотрим кардинал d , отвечающий множеству a \ b . Тогда b + d = a и выполнены соотношения:

a ² = (b + d)² = b ² + 2×b×d + d ² = b + 2×b×d + d ².

Если d < a , то d ² = d и 2×b×d £ 2×g ² = g , где g = max{b , d}. Таким образом, в этом случае a ² = b + 2×b×d + d ² = b + g + d = b + d = a – противоречие. Значит, d = a > b .

Для каждого w £ b < a есть биекция j_b : b ® b ² . На множестве упорядоченных пар (b ; j_b ) введём отношение порядка p : (b ; j_b ) p (g ; j_g ) тогда и только тогда, когда b < g и j_g |_b = j_b . Это отношение частичного порядка. При этом, если (b ; j_b ) p (g ; j_g ) p … – возрастающая цепочка, то у неё есть верхняя грань (u ; j), где u – объединение всех кардиналов b , g , … этой цепочки, а j : u ® u ² продолжает все функции цепочки: j(x) = j_e(x), если x Î e . Такое определение не зависит от выбора e : если x Î t , где (t ; j_t) < (e ; j_e), то j_t(x) = j_e(x), т.к. j_e |_t = j_t . Проверьте, что j – биекция.

По лемме Цорна существует максимальная пара (π ; y), т.е. непродолжаемое биективное отображение y : π ® π ². Ясно, что w < π < a и по доказанному выше x = a – π = a > π . Рассмотрим кардинал π + π = 2×π < a и распространим y до биекции y : 2×π ® (2×π)² : квадрат (2×π)² состоит из четырёх равномощных квадратиков π ² ~ π, причём π = π² £ £ 3×π² = 3×π £ π ² = π , так что существует биекция из отрезка (π; 2×π] на “уголок” из трёх квадратиков (см. рисунок выше). Таким образом, y будет по-прежнему отображать [0; π] на квадратик π ² , а отрезок (π; 2×π] – на “уголок” из трёх таких квадратиков. Построенное продолжение противоречит непродолжаемости y .

20⁰. " a , b Î Сard(U) (a ³ w Ú b ³ w) ® (a + b = max{a, b})

Если a £ b, то a + b £ b + b = 2×b £ b ² = max{a, b} = b £ a + b.

Итак, арифметика кардинальных чисел, с одной стороны, обобщает обычную арифметику натуральных чисел, но, с другой, привносит многие необычные черты в знакомый пейзаж.