Кардинальные числа : порядок

Понятие мощности множества и сравнения мощностей было введено по аналогии с важной характеристикой конечных множеств – числом их элементов. Оказывается, эту аналогию можно сделать ещё более зримой.

Зафиксируем универсальное множество U и будем работать в дальнейшем с его элементами и подмножествами. При этом будем считать, что U достаточно “большое”, т.е. U содержит пустое множествои замкнуто относительно всех теоретико-множественных операций объединения, пересечения, разности, дополнения, взятия булеанов, декартова произведения и степеней:

Æ Î U, " A, B Í U A È B Í U, A Ç B Í U, A \ B Í U, 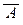Í U,

B(A) Í U, A´B Í U, A^B Í U.

В частности, множество U бесконечно (?!).

Отношение A ~ B равномощности множеств A Í U, B Í U является тогда отношением эквивалентности на множестве B(U). Поэтому множество B(U) разбивается на классы эквивалентности вида = {X Î B(U) | X ~ A}, состоящие из всех подмножеств X Í U , равномощных выделенному представителю класса – множеству A. Так, например, для пустого множества A = Æ класс состоит из одного пустого множества (единственного нульэлементного подмножества множества U), а для одноэлементного множества A = {a₁} класс состоит из всех одноэлементных подмножеств. Вообще, если множество A = {a₁ , … , a_n} состоит из n элементов, то класс состоит из всех n-элементных подмножеств.

Естественно обозначать классы 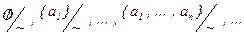символами 0, 1, … , n, … и отождествить эти символы с натуральными числами (с нулём). Аналогично, произвольный класс , состоящий из всех множеств, мощности |A|, будем называть кардинальным числом (или кардиналом), которое, очевидно, являет собой квинтэссенцию понятия мощности |A| £ |U|. Таким образом, фактор-множество 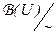= { Î B(B(U)) | A Í U} можно рассматривать как множество кардинальных чисел. Чем шире универсальное множество U, тем больше кардинальных чисел будет построено. Если множество U бесконечно (а имеет смысл рассматривать, конечно, только большие универсальные множества), то получается следующее множество кардинальных чисел

Card(U) = {0, 1, … , n, … , À₀ , … , À₁ , … },

где через w = À₀ обозначен кардинал, соответствующий счётной мощности. Кардинал, соответствующий мощности континуума обозначается, как правило, через с = À₁ . Поскольку R ~ 2^N, то его часто обозначают через .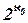

Сразу возникает естественный вопрос: есть ли между À₀ и 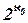промежуточные кардиналы ? Другими словами, может ли существовать множество M со свойствами N Í M Í R и |N| < |M| < |R| ? Это знаменитая континуум-гипотеза. Как доказал в 1960 г. П. Коэн, континуум-гипотеза является примером утверждения, не зависящего от аксиом формальной теории множеств: существуют модели этой теории, в которых есть промежуточные кардиналы, и существуют модели теории множеств, в которых нет таких кардиналов. Можно сформулировать обобщённую континуум-гипотезу: если À_i – некоторый кардинал, отвечающий мощности |А| некоторого множества А, а À_i+1 = 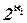– кардинал, отвечающий мощности |B(A)|, то существуют ли промежуточные кардиналы между À_i и À_i+1 ? По всей видимости, для произвольного кардинала À_i ответ тоже независим от аксиоматики теории множеств.