Решение нелинейных уравнений

Иррациональные числа, которые не могут быть корнем никакого алгебраического уравнения с целыми коэффициентами, называют трансцендентными числами. К таким числам относятся корни нелинейных уравнений, которые обычно решаются с помощью операторов IF – GOTO.

Задача в общем виде формируется следующим образом.

Пусть требуется с точностью 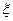определить значение одного из корней нелинейного уравнения 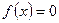, исходя из значения начального приближения корня 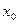. При этом считается, что функция 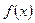удовлетворяет условию, гарантирующим существование решения и сходимость последовательности приближений к точному значения корня.

Известно множество методов вычисления корня уравнения. Все они предлагают приближение к корню по формуле:

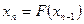, где

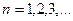
Функция 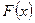учитывает расчетную формулу метода и исходную функцию .

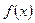Обычно значение 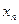считают достаточно хорошим приближением к точному значению корня, если выполняется условие:

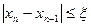
При вычислении этого неравенства искомое значение корня получается равным 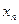, и вычисление прекращается.

Количество циклов приближения неизвестно, поэтому требуется анализ с помощью IF.

Студентам предлагается 3 метода решения нелинейных уравнений: метод простой итерации, метод Ньютона и метод деления пополам (метод бисекций).