Метод деления пополам

Задано: 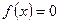, 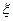и интервал 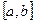, где существует корень.

При использовании этого метода интервал 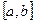изменяется таким образом, чтобы оказался в 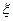-окрестности искомого корня, который может находиться как справа, так и слева от искомого 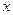. Поэтому условием нахождения искомого корня x следует считать выполнение условия

.

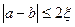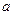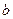Для перемещения или интервала 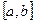используется теорема Больцмана-Коши (о существовании корня внутри интервала):

,

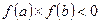т.е. корень существует, если произведение функций при значениях концов интервала является отрицательным.

Алгоритм решения следующий.

1. .

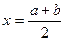2. Вычисляется .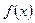

3. Вычисляется 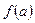(или ).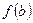

4. Анализ 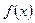. Если 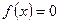, то выход из цикла; в противном случае п.5.

5. Анализ интервала 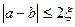. Если условие выполняется, то выход из цикла; в противном случае надо сдвигать интервал по п.6.

6. Анализируется 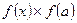. Если 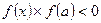, то 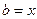; в противном случае .

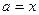7. Вычисления отправляются к п.1 (через GOTO).

Задание 1.

1. Составить схему алгоритма для вычисления функций, приведенных в таблице 5.6.

2. Написать программу на языке BASIC.

3. Произвести расчеты на микроЭВМ.

4. Распечатать листинг программы.

5. Исходные данные, промежуточные и окончательные результаты вывести на экран монитора и на печатающее устройство.

Задание 2.

1. Составить схему алгоритма для вычисления функций, приведенных в таблице 5.7.

2. Выполнить пп. 2 – 5 задания 1.

Таблица 5.6. Список заданий

Вариант	Функции	Исходные данные

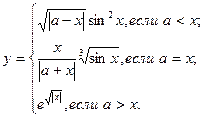
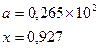
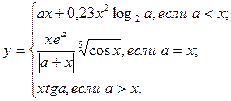
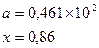
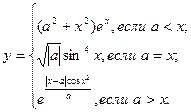
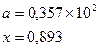
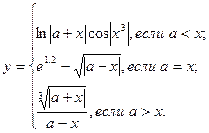
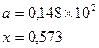
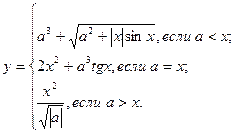
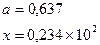
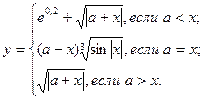
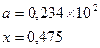
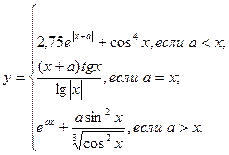
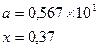
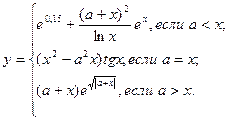
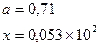
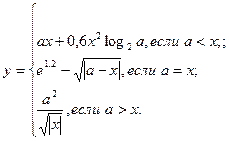
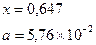
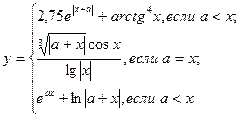
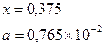
Таблица 5.7. Список заданий

Вариант	Функции	Исходные данные
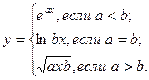	причем х – корень нелинейного уравнения ln x – x + 1,8 = 0, которое необходимо решить методом деления пополам с точностью e.	a = 1 b = 4 c = 3 e = 10-4 Интервал существования корня [1,7; 3,3]
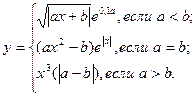	причем х – корень нелинейного уравнения x – sin x = 0,25, которое необходимо решить любым методом с точностью e при начальном значении x0.	a = 2,23 b = 13,12 e = 10-5 x0 = 1,17
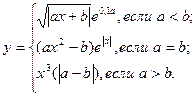	причем х – корень нелинейного уравнения x = e-x, которое необходимо решить методом Ньютона с точностью e при начальном значении x0.	a = 3,17 b = 7,51 e = 10-4 x0 = 0
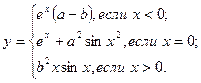	причем х – корень нелинейного уравнения x2 – sin 5x = 0, которое необходимо решить методом Ньютона с точностью e при начальном значении x0.	a = 0,71 b = 2,23 e = 10-3 x0 = 0,58
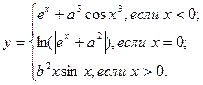	причем х – корень нелинейного уравнения x – sin x = 0,25, которое необходимо решить методом простой итерации с точностью e при начальном значении x0.	a = 1,21 b = 10,01 e = 10-4 x0 = 1,18
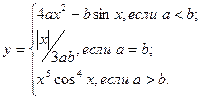	причем х – корень нелинейного уравнения x = e-x, которое необходимо решить методом деления пополам с точностью e.	a = 1,05 b = 10,1 e = 10-5 Интервал существования корня [-1; 1]
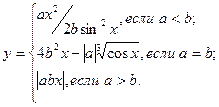	причем х – корень нелинейного уравнения x – sin2 x = 0,25, которое необходимо решить методом простой итерации с точностью e при начальном значении x0.	a = 3,01 b = 8,15 e = 10-4 x0 = 1,16
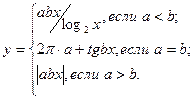	причем х – корень нелинейного уравнения x2 – sin 5x = 0, которое необходимо решить методом деления пополам с точностью e.	a = 2,25 b = 7,15 e = 10-5 x0 = 1,17
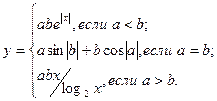	причем х – корень нелинейного уравнения x3 – cos 2x = 0, которое необходимо решить методом Ньютона с точностью e при начальном значении x0.	a = 1,75 b = 3,25 e = 10-5 Интервал существования корня [-5; 2]
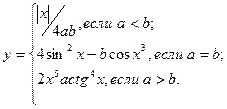	причем х – корень нелинейного уравнения 10x = lnx+ex, которое необходимо решить методом деления пополам с точностью e.	a = 1,96 b = 1,05 e = 10-5 Интервал существования корня [-2,7; 4,3]