Метод простой итерации

Задано: 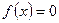, 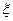и .

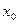Введем обозначения: 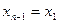, , 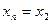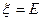. При использовании метода простой итерации уравнение 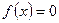необходимо решить относительно 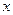в общем виде:

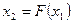
Тогда алгоритм решения будет следующим.

1. Задается значение .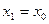

2. Вычисляется .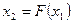

3. Проверяется условие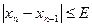

4. Если условие выполняется (“истина”), то 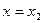в противном случае 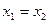и следует повторять цикл с п.2 (через GOTO).

Метод Ньютона

Задано: 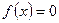, 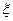и 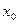. При использовании этого метода нелинейное уравнение должно быть приведено к виду .

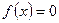Введем обозначения: 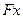- левая часть нелинейного уравнения; 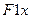– первая производная от ;

.

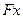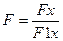Так как вычисления искомого значения 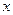производится в этом методе иначе, чем в методе простой итерации, то значения 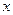могут использоваться без индексов. Анализ нахождения искомого значения 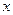можно упростить. Это несложное доказательство оставляется студентам.

Итак, алгоритм решения.

1. Задаем значение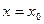

2. Вычисляется .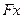

3. Вычисляется .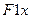

4. Определяется .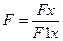

5. Проверяется условие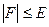

Если условие выполняется, то 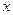- искомый корень, в противном случае следует повторить цикл с п.2.