УРАВНЕНИЕ БЕГУЩЕЙ ВОЛНЫ
СТОЯЧИЕ ВОЛНЫ
Колеблющееся тело — источник колебаний (камертон, струна, мембрана и т. д.), находящееся в упругой среде, приводит в колебательное движение соприкасающиеся с ним частицы среды. Колебание этих частиц передается (силами упругости) соседним частицам среды и т. д. Через некоторое время колебание охватит всю среду. Процесс распространения колебательного движения в среде называется волной. Направление распространения волны (колебаний) называется лучом. Волна называется поперечной, если частицы среды колеблются перпендикулярно лучу. Если колебания частиц среды происходят вдоль луча, волна называется продольной.
Если точка 0 совершает колебательное движение в упругой среде по гармоническому закону (рис. 9):
у = А sin ωt, (39)
где y — смещение колеблющейся точки;
А — амплитуда (наибольшее смещение точки от положения равновесия);
t — время;
Т— период;
ω = 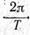 — циклическая или круговая частота. — циклическая или круговая частота.
| 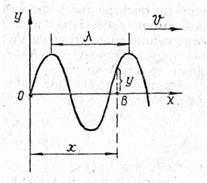 Рис.9 Рис.9
|
Соседняя точка В среды придет в. колебательное движение с некоторым запозданием на время:
τ = 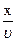 , (40)
, (40)
где х — расстояние, на которое распространилось колебание от точки 0 до точки, В;
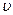 — скорость распространения колебания от 0 до В.
— скорость распространения колебания от 0 до В.
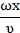 Тогда уравнение колебаний в точке В запишется:
Тогда уравнение колебаний в точке В запишется:
y = А sin ω (1—τ) = А sin (ωt − ) (41)
Соотношение (41), позволяющее определить смещение любой точки среды в любой момент времени, называется уравнением бегущей плоской синусоидальной волны.
Длиной волны(λ)называется расстояние между соседними точками, находящимися в одинаковой фазе, т. е. расстояние, пройденное волной за один период колебания, следовательно:
λ = vT = 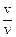 ; v = λν (42)
; v = λν (42)
где ν — частота колебания частиц среды (частота волны). Колебания частиц среды имеют ту же частоту, что и колебания источника волн. Волны, частоты колебаний в которых лежат в пределах от 16 до 20000 Гц, называют звуковыми. В звуковой или акустической волне происходят механические колебания частиц среды с малыми амплитудами.
Подставляя в уравнение (41) v= 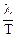 и учитывая, что ω =
и учитывая, что ω = 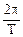 = 2πν, получим другие формы записи уравнения волны:
= 2πν, получим другие формы записи уравнения волны:
y = А sin 2π(t/T—x/λ) = А sin 2π (νt— x/λ) = А sin(ωt - 2π x/λ), (43)
где 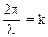 — волновое число, которое показывает, сколько длин волн укладывается на отрезке длиной 2π. Тогда уравнение волны запишется:
— волновое число, которое показывает, сколько длин волн укладывается на отрезке длиной 2π. Тогда уравнение волны запишется:
y = А sin(ω t—kx) (44)
Метод определения скорости звука основан на свойствах звуковой стоячей волны.Стоячие волны образуются при наложении (интерференции) двух встречных плоских волн с одинаковой амплитудой. Практически стоячие волны возникают при отражении волн от преград. Падающая на преграду волна и бегущая навстречу отраженная волна, налагаясь друг на друга, дают стоячую волну.
Напишем уравнение двух плоских волн, распространяющихся вдоль оси X в противоположных направлениях:
y1= А sin (ωt—kx), у2 = А sin (ωt + kx)
Сложив эти уравнения и преобразовав результат по формуле для суммы синусов, получим:
у = y1 + у2 = 2А cos k x sin ωt (45)
Заменим волновое число kего значением 2π/λ. Тогда уравнение (45) примет вид:
у = 2Асоs 2π 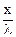 sin ωt (46)
sin ωt (46)
Уравнение (46) есть уравнение стоячей волны. Из этого уравнения видно, что в каждой точке стоячей волны происходят колебания той же частоты, что и у встречных волн, причем амплитуда (у max) зависит от х:
у max = 2А cos 2π 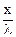
В точках, координаты которых удовлетворяют условию
| (7) |
2π 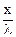 =±nπ (n = 0, 1,2, 3, ...), (47)
=±nπ (n = 0, 1,2, 3, ...), (47)
амплитуда колебаний достигает максимального значения (у max = 2А). Эти точки называются пучностямистоячей волны. Из (47) получаются значения координат пучностей:
xпучн = ± n 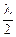 (n = 0,1,2,3,…), (48)
(n = 0,1,2,3,…), (48)
В точках, координаты которых удовлетворяют условию
2π 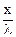 =±(n +
=±(n + 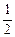 )π (n = 0, 1,2, 3, ...),'
)π (n = 0, 1,2, 3, ...),'
амплитуда колебаний обращается в ноль (у max = 0). Эти точки называются узламистоячей волны. Точки среды, находящиеся в узлах, колебаний не совершают. Координаты узлов имеют значения
| (9) |
xузл = ±(n + 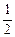 )
) 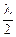 (n = 0, 1,2, 3, ...), (49)
(n = 0, 1,2, 3, ...), (49)
Из формул 48 и 49 следует, что расстояние между соседними пучностями, так же как и расстояние между соседними узлами, равно λ/2. Пучности и узлы сдвинуты друг относительно друга на λ /4.
Дата добавления: 2021-12-14; просмотров: 721;











