ДИФРАКЦИОННАЯ РЕШЕТКА
Экспериментально установлено, что свет в однородной среде распространяется прямолинейно. Однако более детальные наблюдения показывают, что световая волна заходит в область геометрической тени, причем на границе между областями света и тени появляются максимумы и минимумы света, свидетельствующие о некотором перераспределении световой энергии на этой границе.
Огибание световой волной границ непрозрачных тел с образованием интерференционного перераспределения энергии по различным направлениям называется дифракцией света.
Дифракция — доказательство волновой природы света; дифракция свойственна не только световым, но и вообще всяким волнам. Различают с некоторой степенью условности дифракцию сферических волн (дифракция Френеля) и дифракцию плоскопараллельных волн (дифракция Фраунгофера).
Расчет и объяснение дифракции света осуществляется на основе принципа Гюйгенса-Френеля. Согласно принципу Гюйгенса, каждую точку фронта волны можно рассматривать как самостоятельный вторичный источник сферических волн. Построив огибающую всех вторичных источников, находят положение фронта волны в любой последующий момент времени, тем самым определяют направление дальнейшего распространения света. Френель дополнил принцип Гюйгенса рядом интерференционных положений; он ввел представление о когерентности вторичных волн и их интерференции. Для того чтобы определить результат дифракции в некоторой точке пространства, следует рассчитать, согласно принципу Гюйгенса-Френеля, интерференцию вторичных волн,
|
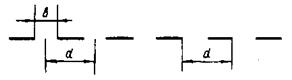
| Рис. 13 |
попавших в эту точку от волновой поверхности (фронта волны, в случае однородной среды).
В лабораторной практике дифракционную картину чаще всего получают от дифракционных решеток. Дифракционная решетка — оптическое устройство, представляющее собой совокупность большого числа параллельных, обычно равноотстоящих друг от друга щелей одинаковой формы. Плоская прозрачная дифракционная решетка — это прозрачная пластина с большим количеством (до 1000 на длине 1 мм) тонких параллельных щелей одинаковой ширины bи равными расстояниями dмежду их серединами (или соответственными точками).Расстояние d называется периодом или постоянной решетки. Условное обозначение дифракционной решетки показано на рис. 13.
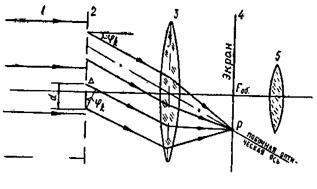
На рис. 14 представлен ход лучей через решетку согласно схеме дифракции Фраунгофера. Параллельный пучок лучей 1, идущих от одного источника, падает на дифракционную решетку 2 перпендикулярно к ней. Эти лучи дифрагируют при прохождении через решетку, образуя (вторичные) когерентные расходящиеся пучки под углами дифракции φ1, φ2,…φk. Пучки, прошедшие объектив 3 зрительной трубы, дают в его фокальной плоскости 4 дифракционную картину, как результат дошедших до плоскости 4 когерентных колебаний. Получающееся изображение можно наблюдать с помощью объектива 5.
Распределение интенсивности в дифракционной картине получим, если учтем распределение интенсивностей при дифракции от одной щели, а также взаимную интерференцию волн от всех щелей. Известно, что каждая щель (в схеме наблюдения дифракции Фраунгофера от нее) дает дифракционную картину, представленную на рис. 15. При этом условие минимумов интенсивности, называемых в данном случае первичными, выражается в виде:
 , ,
| (47) |
| где m=1,2,3,... (при m = 0возникает максимум); | |
| b— ширина щели |
|
Рис. 14
φm— угол дифракции;
λ — длина волны в данной среде.
Условие максимумов:
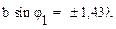 ;
; 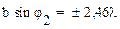 ;
;
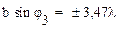 ; … (47а)
; … (47а)
При дифракции от решетки (рис. 14) картины от всех щелей придутся на одно и то же место плоскости 4 (экрана), усиливая друг друга.
Учтем взаимную интерференцию когерентных колебаний, приходящих от различных щелей. Очевидно, условие минимума (47) для одной щели является также условием минимума для решетки: в этих направлениях φ условия «гашения» света выполняются для каждой щели в отдельности, а следовательно, и для всей решетки в целом. Кроме того, из рис. 14 видно, что разность хода Δ лучей, идущих от любых соответственно расположенных пар точек (например, центральных точек) соседних щелей, равна Δ = d sin φ; если эта разность хода кратна целому числу длин волн (четному числу полуволн), то при интерференции возникнут главные максимумы, определяемые условием (2):
 (48)
(48)
где k = 1, 2, 3, ... — порядок дифракционного максимума. Соотношение (48) называется основной формулой дифракционной решетки.
Амплитуда колебаний в точках фокальной плоскости 4 (рис. 14), соответствующих главным максимумам, равна
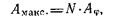 (49)
(49)
где Aφ - амплитуда колебаний, посылаемых одной щелью под утлом φ;
N - число щелей решетки.
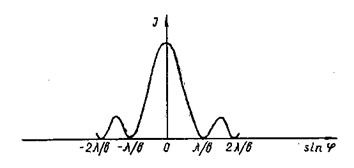 Рис. 15
Рис. 15
Известно, что интенсивность света I прямо пропорциональна квадрату амплитуды волны. Таким образом, интенсивность главных максимумов Iмакс, пропорциональна квадрату числа щелей решетки:
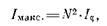 (50)
(50)
где Iφ — интенсивность, создаваемая одной щелью в направлении φ.
Можно доказать, что направления, для которых колебания от отдельных щелей взаимно погашают друг друга, т. е. добавочные минимумы удовлетворяют следующему условию:
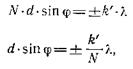
или
(k΄ = 1, 2, …, N – 1, N + 1,…)
Между двумя главными максимумами возникает (N—1) минимумов. Между этими минимумами должны находиться побочные (дополнительные) максимумы, в которых интенсивность света при достаточно большом N пренебрежимо мала по сравнению с интенсивностью главных максимумов.
Результирующее распределение интенсивности в дифракционной картине от решетки представлено на рис. 16. Пунктирная кривая дает интенсивность от одной щели, умноженную на N2. Сплошная кривая соответствует главным максимумам, а также добавочным максимумам и минимумам.
С помощью дифракционной решетки можно анализировать свет, т. е. изучать его спектральный состав. Действительно, в том случае, когда источник излучает немонохроматический свет (например, белый), то решетка разлагает его в спектр. При φ0 = 0 возникает максимум нулевого порядка, совпадающий для всех длин волн. По обе стороны от него возникнут спектры — максимумы порядков ±k. В спектре каждого порядка максимумы для более коротких волн расположатся ближе к нулевому максимуму. Максимумы для более длинных волн — дальше от него.
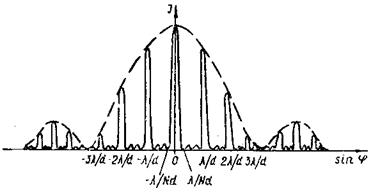 Рис. 16
Рис. 16
Способность дифракционной решетки разлагать свет в спектр позволяет использовать ее как диспергирующее устройство в спектральных приборах.
Дата добавления: 2021-12-14; просмотров: 583;











