ИНТЕРФЕРЕНЦИЯ СВЕТА
По современным научным представлениям, свет — это сложный электромагнитный процесс, обладающий как волновыми, так и корпускулярными свойствами. Настоящая работа базируется на наблюдении и изучении явления интерференции света, которое объясняется с позиций волновой теории света.
Интерференцией света называется такое сложение световых волн, в результате которого образуется устойчивая картина их усиления и ослабления.
НАЧАТЬ С → ↓
Рис. 10, формула 50
Для осуществления интерференции накладывающиеся волны должны удовлетворять условиям когерентности (согласованности по фазе световых колебаний в пучках света или отдельных частях пучка). Когерентными называются волны, имеющие одинаковые частоты и постоянную во времени разность фаз.
Реальные светящиеся тела испускают некогерентные волны. Так происходит потому, что поверхность любого светящегося тела состоит из множества точек (атомов), автономно, прерывно и случайным образом излучающих световые волны. Понятно, что никакой согласованности по фазе между такими волнами нет. Для получения когерентных световых пучков применяют различные искусственные приемы, в основе которых лежит разделение одного и того же пучка на два, идущих впоследствии к какой-либо точке пространства (экрана) двумя различными путями. В зависимости от способа разбиения пучка существует два разных метода получения когерентных «источников»:
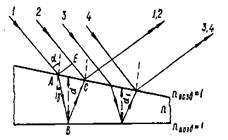
| 1) метод деления волнового фронта, когда исходящий от источника пучок делится на два, либо проходя через два близко расположенных отверстия, либо отражаясь от зеркальных поверхностей и т. д.; |
| Рис. 10 |
2) метод деления амплитуды, который предполагает деление пучка путем прохождения и отражения от полупрозрачной поверхности. Именно этот способ рассматривается в настоящем разделе; в результате чего получается интерференционная картина, называемая кольцами Ньютона.
Разделение луча (пучка) на два когерентных осуществляется путем его отражения от поверхностей тонкого прозрачного слоя (рис. 10): Пусть параллельный монохроматический пучок света от одного источника падает на клиновидный слой; выделим из него два луча — 1 и 2 (или любую другую пару лучей — 3 и 4). Проведем перпендикулярно лучам плоскость АЕ, которая является фронтом падающей волны (до плоскости АЕ два луча — 1 и 2, идущие от одного источника, дошли одновременно, а следовательно, имели нулевую разность фаз). От плоскости АЕ лучи прошли различные пути; в точке С произошло сложение колебаний, результат которого будет зависеть от разности фаз складывающихся волн.
Разность фаз связана с разностью хода δ лучей соотношением:
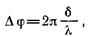 (39)
(39)
где
 длина волны падающего света;
длина волны падающего света;
оптическая разность хода лучей;
геометрическая разность хода лучей ;
абсолютный показатель преломления
Оптическая разность хода δ лучей 1 и 2 в рассматриваемом случае выразится в виде:
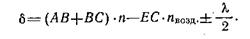
|
(40)
Член π/2 возникает соответственно «потере» фазы (запаздыванию) на π при отражении света от оптически более плотного слоя диэлектрика в оптически менее плотный. Знак плюс или минус берется в зависимости от того, где происходит указанное отражение. Очевидно, в данном случае следует взять знак минус (клин находится в воздухе, отражение от более плотной среды происходит в точке С, следовательно, «теряет» фазу отраженный луч 2). Приблизительно полагая в формуле (40) АВ = ВС = = d и ЕС=0 (поскольку падающий пучок света узкий и все лучи 1, 2, 3, 4 и т. д. практически совпадают), получаем следующее выражение для оптической разности хода:
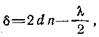 (41)
(41)
где d— толщина клина в точке В.
'Интерференционные максимумы и минимумы будут иметь такой вид:
2dn - 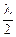 =kλ = 2k
=kλ = 2k 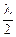 (41a максимум);
(41a максимум);
2dn - 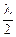 = (2k—1)
= (2k—1) 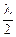 (41б минимум),
(41б минимум),
где k = 0,1,2,...— порядок интерференционного максимума и минимума.
Из формул (41) видно, что всем точкам поверхности пластинки одинаковой толщины соответствует одна и та же интерференционная картина: максимумы или минимумы одинаковой интенсивности. Интерференционная картина имеет вид полос светлых и темных, их называют полосами (линиями) равной толщины. Этот вид интерференции называется интерференцией равной толщины. В случае клиновидного слоя полосы будут параллельны ребру клина (рис. 11). При использовании белого (полихроматического) света интерференционные полосы приобретают радужную окраску (всем известны цвета тонкой масляной или керосиновой пленки на воде или на стекле). Это происходит потому, что разность хода б (формулы (41)) зависит и от длины волны, а следовательно, при одной и той же толщине пластинки dмаксимумы и минимумы для волн различных длин будут несколько сдвинуты относительно друг друга.
Интерференцию можно также наблюдать в проходящем через пластинку свете.
В зависимости от формы пластинки меняется и форма интерференционных полос. Следует заметить, что в реальных условиях падающие лучи не идеально параллельны, грани пластинки искривлены, толщина неравномерно меняется, показатель преломления тоже, меняется на неоднородностях материала и т. д. По всем этим, многочисленным причинам будут наблюдаться причудливо изогнутые линии, вид которых дает возможность судить очень точно о толщине пластинки в данной точке или о неоднородностях материала (интерференционные методы измерения — одни из самых точных).
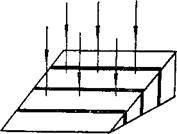
| В случае когда сферическая линза наложена на плоское стекло (рис. 3), роль пластинки переменной толщины играет воздушный слой (n возд = 1) между линзой и плоской пластинкой, а интерференционные полосы равной толщины |
| Рис. 11 |
образуют концентрические окружности с темным пятном (минимумом) в середине. Эта интерференционная схема представляет собой схему колец Ньютона.
На основании формулы (40) и следующих за ней рассуждений будем здесь иметь:
δ = 2dl + 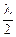 = 2d +
= 2d + 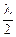 (42)
(42)
Учитывая условия (41) совместно с (42), покажем, при каких значениях d возникают светлые и темные интерференционные кольца в данной схеме:
dk = 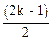
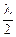 (42а, максимум)
(42а, максимум)
dk = kλ = 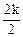
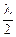 (42б, минимум)
(42б, минимум)
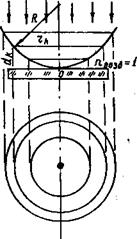
откуда и следует, что максимума нулевого порядка не будет, т. е. в отраженном свете в схеме колец Ньютона наблюдается темное пятно (рис. 12).
Длина световой волны может быть определена на основании рис. 12:
R2 = 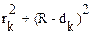 или
или
| 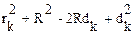 (43)
Отсюда с учетом того, что толщина d невелика и член d2является пренебрежимо малым, получаем: (43)
Отсюда с учетом того, что толщина d невелика и член d2является пренебрежимо малым, получаем:
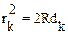 (44)
Подставим в (44) значение dk (минимум) из формул (42): (44)
Подставим в (44) значение dk (минимум) из формул (42):
 = kλR, т. е. = kλR, т. е.
|
| Рис.12 |
λ =  (45)
(45)
где rk— радиус интерференционного кольца — минимума k-того порядка;
R— радиус сферы линзы.
Так как обеспечить контакт в точке О (рис. 12) трудно вследствие попадания пылинок, то пользуются другой формулой, в которую входит комбинация из двух значений радиусов интерференционных колец rk и гг-, что позволяет исключать возможный зазор (т. е. реально существующее увеличение толщины всего воздушного слоя) в точке 0, Для i-того и k-того колец можно записать:
 = kλR;
= kλR;
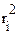 = iλR
= iλR
Вычтем почленно эти уравнения:
 = (k - i) λR откуда
= (k - i) λR откуда
λ =  , (46)
, (46)
где k и i — порядки интерференционных колец.
Формула (46) остается одной и той же как для интерференционных минимумов, так и для максимумов.
Точность определения λ по формуле (46) зависит от того, насколько точно измерены rk и ri, а так как последние величины являются очень малыми, то для их измерения пользуются микроскопом. Кроме того, для понижения погрешности следует выбрать rk и ri таким образом, чтобы числа k и i были возможно дальше друг от друга.
Дата добавления: 2021-12-14; просмотров: 397;











