ЗАКОНЫ ОТРАЖЕНИЯ И ПРЕЛОМЛЕНИЯ СВЕТА
Раздел оптики, в котором законы распространения света рассматриваются на основе представления о световых лучах, называется геометрической оптикой. Под световыми лучами понимают нормальные к волновым поверхностям линии, вдоль которых распространяется поток световой энергии.
На границе раздела двух прозрачных однородных сред свет частично отражается, а частично проходит во вторую среду, изменяя при этом свое направление. Закон отражения: отраженный луч лежит в одной плоскости с падающим лучом и перпендикуляром, проведенным к границе раздела двух сред в точке падения; угол отражения α равен углу падения β:
α = β (1)
Направление распространения светового луча в этих средах определяется законом преломления Снеллиуса: преломленный луч лежит в той же плоскости, в которой находятся падающий луч и нормаль к разделу сред, восстановленная в точке падения; отношение синуса угла падения (α) и угла преломления (γ) есть величина постоянная для данной пары сред:
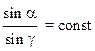 (2)
(2)
Значение постоянной величины (const) можно определить из волновой теории света (рис. 1). Пусть «ММ» - граница двух сред, в которых свет распространяется с разными скоростями v1 и v2 (причем v1 > v2). Под некоторым углом α на границу ММ падает параллельный пучок световых лучей. Выберем в этом потоке два луча SA и SB. AC – фронт падающих лучей. Согласно принципу Гюйгенса, каждую точку волнового фронта следует рассматри-
 ватькак самостоятельный источник новых волн. Следовательно, но, пока второй луч SB дойдет до точки В, около точки А возникает полусферическая волна с радиусом AD, причем AD < CB, т. к. v2 < v1. Фронтом новой волны по принципу Гюйгенса будет ВD – касательная, проведенная из точки B к AS′ – направлению преломленного луча, поэтому BD ┴ ADS′. Угол между нормалью к границе ММ и преломленным лучем ADS′ – угол преломления γ. Из геометрических соображений (углы, образованные взаимноперпендикулярными сторонами) угол САВ равен углу α, угол ADB равен углу γ. Из прямоугольных треугольников АСВ и ADB можем написать: СВ = АВ·sin α ; AD = AB · sin α. Разделив эти уравнения, получим:
ватькак самостоятельный источник новых волн. Следовательно, но, пока второй луч SB дойдет до точки В, около точки А возникает полусферическая волна с радиусом AD, причем AD < CB, т. к. v2 < v1. Фронтом новой волны по принципу Гюйгенса будет ВD – касательная, проведенная из точки B к AS′ – направлению преломленного луча, поэтому BD ┴ ADS′. Угол между нормалью к границе ММ и преломленным лучем ADS′ – угол преломления γ. Из геометрических соображений (углы, образованные взаимноперпендикулярными сторонами) угол САВ равен углу α, угол ADB равен углу γ. Из прямоугольных треугольников АСВ и ADB можем написать: СВ = АВ·sin α ; AD = AB · sin α. Разделив эти уравнения, получим:
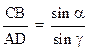 (3)
(3)
Теперь разделим числитель и знаменатель левого отношения равенства (3) на промежуток времени Δt, за который свет проходит путь СВ в первой среде и путь AD во второй среде:
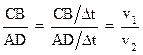 (4)
(4)
Объединив уравнения (3) и (4), получим:
 (5)
(5)
Так как абсолютный показатель преломления среды (n) равен отношению скорости света (с) в вакууме к скорости света (v) в данной среде, то можно записать:
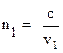 и
и 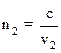 (6)
(6)
Равенство (4) с учетом формул (5) примет вид:
 (7)
(7)
где n21 - относительный показатель преломления двух сред. Соотношение (7) – закон преломления света на границе двух сред.
Показатель преломления является важной индивидуальной физической характеристикой вещества. Он принадлежит к тем физическим величинам, которые можно измерить с высокой степенью точности и небольшой затратой времени, располагая малым количеством вещества.
Оптические методы исследования веществ, основанные на измерении их показателей преломления, составляют самостоятельный раздел прикладной оптики – рефрактометрию. Рефрактометрические данные можно использовать для определения чистоты вещества и концентрации вещества в растворе, для идентификации различных веществ и т. п.
При переходе света (рис. 2а) из среды с меньшим показателем преломления (оптически менее плотная) в среду с большим показателем преломления (оптически более плотная) угол падения больше угла преломления

| 
|
Рис 2
(лучи 1 и 1′). Если угол падения луча 2 близок к прямому (α = 90˚, луч ْ2 скользит вдоль границы раздела сред), то он будет преломляться под углом γпр (луч 2′). Этот угол является наибольшим углом преломления для данных сред и называется предельным углом преломления. Из закона преломления следует:
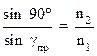 или
или 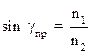 (8)
(8)
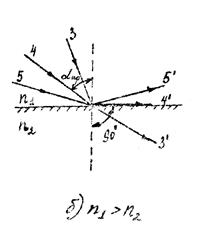
Если свет переходит из оптически более плотной среды в оптически менее плотную (рис. 2б), то угол преломления больше угла падения (лучи 3 и 3′). При некотором угле падения αпр (луч 4) угол преломления равен 90˚, т. е. преломленный луч 4′ скользит вдоль границы сред. При дальнейшем увеличении угла падения света луч 5 полностью отражается (луч 5′) от границы сред возникает явление полного внутреннего отражения. Из формулы (7):
 или
или 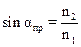 (9)
(9)
Угол αпр называется предельным углом полного отражения. Из формул (8) и (9) следует, что γпр и αпр для данных сред зависят от их абсолютных показателей преломления. Это применяется на практике в приборах для измерения показателя преломления веществ – рефрактометрах.
ЛУПА И МИКРОСКОП
Линзы представляют собой прозрачные тела, ограниченные двумя поверхностями (одна из них обычно сферическая, иногда цилиндрическая, а вторая сферическая или плоская), преломляющими световые лучи, способные формировать оптические изображения предметов. Материалом для линз служат стекло, кварц, кристаллы, пластмассы и т. п. По внешней форме линзы делятся на: 1) двояковыпуклые; 2) плосковыпуклые; 3) двояковогнутые; 4) плосковогнутые; 5) выпукло-вогнутые; 6) вогнуто-выпуклые. По оптическим свойствам линзы делятся на собирающие и рассеивающие. Линза называется тонкой, если ее толщина (расстояние между ограничивающими поверхностями) значительно меньше по сравнению с радиусами поверхностей, ограничивающих линзу. Формула тонкой линзы:

Фокусное расстояние линзы:
f =  (11)
(11)
Точки F, лежащие по обе стороны линзы на расстоянии, равном фокусному, называются фокусами линзы. Фокус − это точка, в которой после преломления собираются все лучи, падающие на линзу параллельно главной оптической оси (прямая, проходящая через центры кривизны поверхностей линзы).

Величина Ф, рассчитываемая по формуле (12) называется оптической силой линзы. Диоптрия − оптическая сила линзы с фокусным расстоянием 1 м: 1 дптр = 1/м. Линзы с положительной силой являются собирающими, с отрицательной − рассеивающими.
Учитывая (12) формулу тонкой линзы можно записать в виде:

Микроскоп является одним из важнейших лабораторных приборов в биологических и медицинских исследованиях. Микроскоп широко применяется для наблюдений и исследования таких объектов, которые невозможно различить невооруженным глазом.
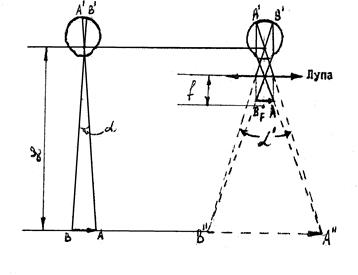
Глаз человека – сложная и совершенная оптическая система. Особенности строения глаза и получения изображения объекта на сетчатке глаза подробно разбираются в указанной литературе. В целом оптическая система глаза действует как собирающая линза с переменным фокусным расстоянием. Размер изображения на сетчатке глаза определяется углом зрения α (рис. 3а). Однако для малых (или удаленных) предметов угол зрения мал и детали предмета выявляются недостаточно.
|
| (а) (б) Рис. 3 |
Оптические приборы, вооружающие глаз, позволяют увеличить угол зрения и поэтому более подробно различать детали предмета. Достигаемый при этом эффект характеризуется угловым увеличением Г прибора:
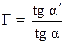 (14)
(14)
где α′ и α – углы зрения, под которым виден предмет соответственно через прибор и невооруженным глазом.
Простейшим оптическим прибором для рассматривания мелких предметов является лупа. Роль лупы выполняют также окуляры оптических приборов – микроскопа, спектроскопа, поляриметра и др.
Лупа – собирающая короткофокусная линза, которую располагают между предметом и глазом. Если невооруженным глазом рассматривать предмет АВ (рис. 3а) с расстояния наилучшего (ясного) зрения L =25 см, то он будет виден под углом α, причем

Поскольку глаз на практике располагают вблизи заднего фокуса лупы (рис. 3б), можно считать, что 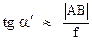 .
.
Подставив полученные значения tg α и tg α′ в формулу (1), получим выражение для углового увеличения лупы:
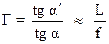 (15)
(15)
Увеличение лупы обратно пропорционально ее фокусному расстоянию и показывает, во сколько раз увеличивается линейный размер изображения на сетчатке за счет применения лупы. На практике используются лупы не бо-
лее 20 – кратного увеличения (20x). Более короткофокусные линзы дают искаженное изображение.
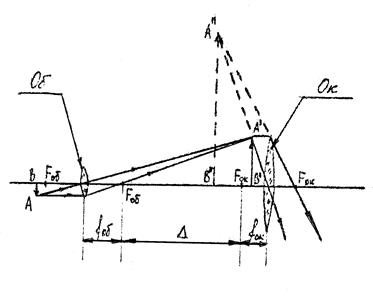
Оптическая система микроскопа состоит из объектива и окуляра, расположенных друг от друга на расстоянии 15 – 20 см на рисунке 4 схематически показан ход лучей в микроскопе.
Предмет АВ помещают чуть дальше переднего фокуса Fоб объектива Об, который дает действительное обратное и увеличенное изображение А′В′. Это промежуточное изображение попадает между окуляром Ок и его передним фокусом Fок . Его рассматривают через окуляр как через лупу. Окончательное изображение А′′В′′ получается
мнимым, увеличенным и прямым относительно А′В′, но обратным относительно самого предмета АВ. Положение объектива относительно предмета подбирается так, чтобы
|
| Рис. 4 |
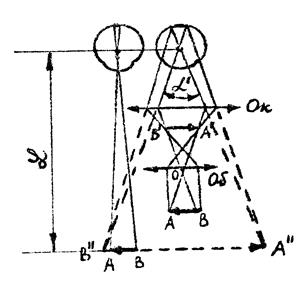
окончательное изображение А′′В′′ располагалось от глаза на расстоянии наилучшего (ясного) зрения L =25 см (рис. 5, на котором для наглядности не соблюдены относительные размеры основных параметров). Качество изображения во многом зависит от объектива. Хорошие объективы, в которых устранены недостатки, состоят из многих линз (иногда более 10), заключенных в общую оправу. Окуляр и объектив биологического микроскопа являются съемными и размещены на концах цилиндрической трубки – тубуса, укрепленного на массивном штативе. Расстояние между внутренними фокусами объектива и окуляра называется оптической длиной тубуса. Оптическая длина Δ тубуса короче его геометрической длины на сумму фокусных расстояний объектива и окуляра.
|
| Рис. 5 |
Увеличение Г микроскопа равно произведению увеличений объектива и окуляра:
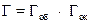 (16)
(16)
Окуляр используется как лупа, и его увеличение определяется формулой:
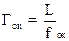 (17)
(17)
Увеличение объектива можно найти, рассматривая подобные треугольники ОАВ и ОА′В′ (см. рис. 4 и 5) и учитывая, что Δ >> fоб:
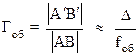 (18)
(18)
Следовательно, угловое увеличение микроскопа:
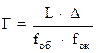 (19)
(19)
Объективы биологических микроскопов имеют угловое увеличение от 8х до 90х, окуляры – от 7х до 15х. Следовательно (см. формулу 16), угловое увеличение микроскопа лежит в пределах от 56х до 1350х. Угловое увеличение оптического микроскопа свыше 1000х использовать нецелесообразно, так как при этом ухудшается качество изображения.
Линейным или поперечным увеличением К называется отношение линейных размеров (см. рис. 5) изображения X2 = |A''B''| предмета X1 = |AB|:
 (20)
(20)
Дата добавления: 2021-12-14; просмотров: 447;











