Особые случаи в применении критерия
1. В случае, если число степеней свободы ν=l, т. е. если признак принимает всего 2 значения, необходимо вносить поправку на непрерывность[15].
2. Если признак варьирует в широком диапазоне (например, от 10 до
140 сек. и т.п.), возникает необходимость укрупнять разряды.
Особый случай 1: поправка на непрерывность для признаков, которые принимают всего 2 значения
Поправка на непрерывность вносится при следующих условиях: а) когда эмпирическое распределение сопоставляется с равномерным распределением, и количество разрядов признака k=2, a ν=k—1=1;
б) когда сопоставляются два эмпирических распределения, и количество разрядов признака равно 2, т.е. и количество строк k=2, и количество столбцов с=2, и ν=(k—l)*(c—1)=1.
Вариант "а": поправка на непрерывность при сопоставлении эмпирического распределения с равномерным. Это тот случай сопоставлений, когда мы, говоря простым языком, проверяем, поровну ли распределились частоты между двумя значениями признака.
Пример с поправкой на непрерывность.
В исследовании порогов социального атома[16] профессиональных психологов просили определить, с какой частотой встречаются в их записной книжке мужские и женские имена коллег-психологов. Попытаемся определить, отличается ли распределение, полученное по записной книжке женщины-психолога X, от равномерного распределения. Эмпирические частоты представлены в Табл. 4.9
Таблица 4.9
Эмпирические частоты встречаемости имен мужчин и женщин в записной книжке психолога X

Сформулируем гипотезы.
Н0: Распределение мужских и женских имён в записной книжке X не отличается от равномерного распределения.
H1: Распределение мужских и женских имен в записной книжке X отличается от равномерного распределения.
Количество наблюдений n=67; количество значений признака k=2. Рассчитаем теоретическую частоту:
Число степеней свободы ν=k -1=1.
Далее все расчеты производим по известному алгоритму, но с одним добавлением: перед возведением в квадрат разности частот мы должны уменьшить абсолютную величину этой разности на 0,5 (см. Табл. 4.10, четвертый столбец).
Таблица 4.10
Расчет критерия % при сопоставлении эмпирического распределения имен с теоретическим равномерным распределением
| Разряды – принадлежность к тому или иному полу | Эмпирическая частота взгляда (fэj) | Теоретическая частота (fт) | (fэj-fт) | (fэj-fт-0,5) | (fэj-fт-0,5)2 | (fэj-fт-0,5)2/ fт | |
| Мужчины Женщины | 33,5 33,5 | -11,5 +11,5 | 3,61 3,61 | ||||
| Суммы | 7,22 | ||||||
Для ν=l определяем по Табл. IX Приложения 1 критические значения:
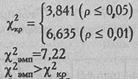
Ответ: Н0 отклоняется, принимается Н1. Распределение мужских и женских имен в записной книжке психолога X отличается от равномерного распределения (р<0,01).
Вариант "б": поправка на непрерывность при сопоставлении двух эмпирических распределений
Попытаемся определить, различаются ли распределения мужских и женских имен у психолога X и психолога С, тоже женщины. Эмпирические частоты приведены в Табл. 4.11.
Таблица 4.11
Эмпирические частоты встречаемости имен мужчин и женщин в записных книжках психолога X. и психолога С.
| Мужчин | Женщин | Всего человек | |
| Психолог Х. Психолог С. | 22 А 59 В | 45 Б 109 Г | |
| Суммы |
Сформулируем гипотезы. H0: Распределения мужских и женских имен в двух записных книжках
не различаются.
H1: Распределения мужских и женских имен в двух записных книжках различаются между собой. Теоретические частоты рассчитываем по уже известной формуле:
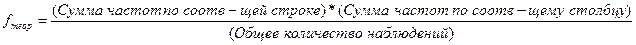
А именно, для разных ячеек таблицы эмпирических частот,
fА теор=67*81/235=23,09
fб теор =67*154/235=43.91
fВ теор=168*81/235=57,91
fГ теор=168*154/235=110,09
Число степеней свободы ν=(k—1)*(с—1)=1 Все дальнейшие расчеты проводим по алгоритму (Табл. 4.12)
Таблица 4.12
Расчет критерия при сопоставлении двух эмпирических распределений мужских и женских имен
| Ячейки таблицы эмпирических частот | Эмпирическая частота взгляда (fэj) | Теоретическая частота (fт) | (fэj-fт) | (fэj-fт-0,5) | (fэj-fт-0,5)2 | (fэj-fт-0,5)2/ fт | |
| А Б В Г | 23,09 43,91 57,91 110,09 | -1,09 +1,09 +1,09 -1,09 | 0,59 0,59 0,59 0,59 | 0,35 0,35 0,35 0,35 | 0,015 0,008 0,006 0,003 | ||
| Суммы | 235,00 | 0,032 | |||||
Критические значения χ2 при ν=l нам известны по предыдущему примеру:
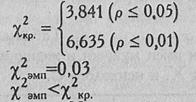
Ответ: Н0 принимается. Распределения мужских и женских имен в записных книжка двух психологов совпадают.
Поправки на непрерывность и всех остальных подсчетов можно избежать, если использовать по отношению к подобного рода задачам метод φ* Фишера (см. параграф 5.4).
Дата добавления: 2016-06-05; просмотров: 1698;











