Пример с укрупнением разрядов признака
Тест Мюнстерберга для измерения избирательности перцептивного внимания в адаптированном варианте М.Д. Дворяшиной (1976) предъявлялся студентам факультета психологии Ленинградского университета (n1=156) и артистам балета Мариинского театра (n2=85). Материал методики состоит из бланка с набором букв русского алфавита, в случайном порядке перемежающихся. Среди этого фона скрыто 24 слова разной степени сложности: "факт", "хоккей", "любовь", "конкурс", "психиатрия" и т.п. Задача испытуемого возможно быстрее отыскать их и подчеркнуть (Дворяшина М.Д., 1976, с. 124). Совпадают ли распределения количества ошибок (пропусков слов) в двух выборках (Табл. 4.13)?
Таблица 4.13
Эмпирические частоты пропуска слов в тесте Мюнстерберга в двух выборках испытуемых (по данным М.Д. Дворяшиной, Е.В. Сидоренко, 1973)
| разряды | Эмпирические частоты пропуска слов | ||
| В группе студентов (n1=156) | В группе артистов балета (n2=85) | Суммы | |
| I. 0 пропусков II. 1 пропуск III. 2 пропуска IV. 3 пропуска V. 4 пропуска VI. 5 пропусков VII. 6 пропусков VIII. 7 пропусков IX. 8 пропусков X. 9 пропусков | |||
| Суммы |
Сформулируем гипотезы.
Н0: Распределения ошибок (пропусков слов) в выборках студентов и артистов балета не различаются между собой.
H1: Распределения ошибок (пропусков слов) в выборках студентов и артистов балета различаются между собой.
Прежде чем перейти к расчету теоретических частот, обратим внимание на последние 4 значения признака, от 6 пропусков и ниже. Очевидно, что fтеор для любой из ячеек последних 4 строк таблицы будет меньше 5. Например, для ячейки, отмеченной кружком:
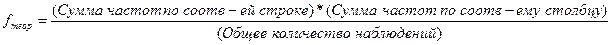 fтеор=5*85/241=1,763
fтеор=5*85/241=1,763
Полученная теоретическая частота меньше 5.
Для того, чтобы решить, какие разряды нам следует укрупнить, чтобы fтеор была не меньше 5, выведем формулу расчета минимальной суммы частот по строке по формуле:
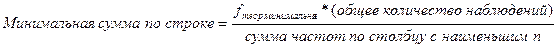
В данном случае столбцом с наименьшим количеством наблюдений является столбец, относящийся к выборке артистов балета (n=85). Определим минимальную сумму частот для каждой строки: Минимальная сумма по строке =5*241/85=14,16 Мы видим, что для получения такой суммы нам недостаточно объединения последних 4 строк Табл. 4.13, так как сумма частот по ним меньше 14 (5+3+2+1=11), а нам необходима сумма частот, превышающая 14. Следовательно, придется объединять в один разряд пять нижних строк Табл. 4.13: теперь любое количество пропусков от 5 до 9 будет составлять один разряд.
Однако это еще не все. Мы видим, далее, что в строке "4 пропуска" сумма составляет всего 8. Значит, ее необходимо объединить со следующей строкой. Теперь и 3, и 4 пропуска будут входить в один разряд. Все остальные суммы по строкам больше 14, поэтому мы не нуждаемся в дальнейшем укрупнении разрядов.
Эмпирические частоты по укрупненным разрядам представлены в Табл. 4.14.
Таблица 4.14
Эмпирические частоты пропуска слов по укрупненным разрядам в двух выборках испытуемых
| Разряды | Эмпирические частоты пропуска слов | ||||
| В группе студентов (n1=156) | В группе артистов балета (n2=85) | Суммы | |||
| I. 0 пропусков II. 1 пропуск III. 2 пропуска IV. 3-4 пропуска V. 5-9 пропусков | А В Д Ж И | Б Г Е З К | |||
| Суммы | |||||
Исследователю бывает огорчительно терять информацию, заведомо утрачиваемую при укрупнении разрядов. Например, в данном случае нас может интересовать, удалось ли сохранить специфический для второй выборки спад частот на 3 и 4 пропусках и резкий их подъем на 5 пропусках (Рис. 4.7).
Сравним графики на Рис. 4.7 и Рис. 4.8. Мы видим, что спад частот во второй выборке на 3-х и 4-х пропусках сохранился, а спад на 2-х пропусках в первой выборке стал еще более заметным. В то же время все возможные различия в частотах в диапазоне от 5-и до 9-и пропусков теперь оцениваются только глобально, по соотношению общих сумм частот в этих диапазонах. По графику на Рис. 4.8 мы уже не можем определить, какое максимальное количество пропусков встречается в первой группе и какое - во второй. Сопоставление распределений на этом конце становится более грубым.


Если бы у нас было больше испытуемых в выборке артистов балета, то, возможно, удалось бы сохранить подъем частоты на 5-и пропусках. Сейчас же нам придется довольствоваться сопоставлением по данным укрупненным разрядам.
Перейдем к подсчету теоретических частот для каждой ячейки Табл. 4.14
fА теор=115*156/241=74,44
fБ теор=115*85/241=40,56
fВ теор=47*156/241=30,41
fГ теор=47*85/241=16,59
fД теор=27*156/241=17,47
fЕ теор=27*85/241=9,53 fЖ теор=27*156/241=17,47
fЗ теор=27*85/241=9,53 fИ теор=25*156/241=16,18 fК теор=25*85/241=8,82
Определим количество степеней свободы V по формуле: ν=(k-l)*(c- l) где k - количество строк (разрядов),
с - количество столбцов (выборок). Для данного случая: ν=(5-l)*(2-l)=4
Все дальнейшие расчеты произведем в таблице по Алгоритму 13. Поправка на непрерывность не требуется, так как v>l.
Таблица 4.15
Расчет критерия χ2 при сопоставлении двух эмпирических распределений пропусков слов в тесте Мюнстерберга (n1=156, n2=85)
| Ячейки таблицы частот | Эмпирическая частота взгляда (fэj) | Теоретическая частота (fт) | (fэj-fт) | (fэj-fт)2 | (fэj-fт)2/ fт |
| А Б В Г Д Е Ж З И К | 74,44 46,56 30,41 16,59 17,47 9,53 17,47 9,53 16,18 8,82 | 18,56 -18,56 -3,41 3,41 -6,47 6,47 2,53 -2,53 -11,18 11,18 | 344,47 344,47 11,63 11,63 41,86 41,86 6,401 6,401 124,99 124,99 | 4,63 8,49 0,38 0,70 2,40 4,40 0,37 0,67 7,72 14,17 | |
| Суммы | 0,00 | 43,95 |
По Табл. IX Приложения 1 определяем критические значения при ν =4:
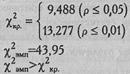
Ответ: Н0 отвергается. Принимается Н1. Распределения про-пусков слов в выборках студентов и артистов балета различаются между собой (р<0,01).
В распределении ошибок у артистов балета можно заметить два выраженных максимума (0 пропусков и 5 пропусков), что может указывать на два возможных источника ошибок[17].
4.3. λ - критерий Колмогорова-Смирнова
Дата добавления: 2016-06-05; просмотров: 1782;











