Примеры формальных аксиоматических теорий
I. Формальное исчисление высказываний. Алфавитэтой теории – это алфавит исчисления высказываний. Онсостоит из трёх групп символов: пропозициональных переменных: a, b, c, d, … , б345 , v964 , … , логических связок: 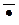 , Ù , Ú , ® , « и служебных символов: ( , ).
, Ù , Ú , ® , « и служебных символов: ( , ).
Правила построения формул исчисления высказыванийизвестны:
(Ф1): любая пропозициональная переменная является формулой.
(Ф2): если A и В – формулы, то (A Ù B), (A Ú B), (A ® B), (A « B), 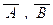 – тоже формулы.
– тоже формулы.
(Ф3): других формул нет.
Аксиомы формального исчисления высказыванийделятся на четыре группы схем аксиом, включающие 11 схем. Это значит, что в нижеследующих псевдоформулах буквы A , B , C – не символы алфавита теории, вместо них можно подставлять любые формулы исчисления высказываний. Таким образом, эти 11 схем аксиом на самом деле представляют бесконечное количество аксиом.
Группа аксиом импликации:
(И1): (A ® (B ® A))
(И2): ((A ® (B ® C)) ® ((A ® B) ® (A ® C)))
Группа аксиом конъюнкции:
(К1): ((A Ù B) ® A)
(К2): ((A Ù B) ® B)
(К3): ((A ® B) ® ((A ® C) ® (A ® (B Ù C))))
Группа аксиом дизъюнкции:
(Д1): (A ® (A Ú B))
(Д2): (B ® (A Ú B))
(Д3): ((A ® C) ® ((B ® C) ® (A Ú B ® C)))
Группа аксиом отрицания:
(О1): (A ® 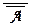 )
)
(О2): ( 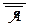 ® A)
® A)
(О3): ((A ® B) ® ( 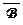 ®
® 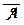 ))
))
В дальнейшем будем опускать в формулах некоторые скобки, предполагая, что их можно расставить по правилам восстановления скобок § 3 главы I.
В приведённом списке аксиом отсутствует логическая связка « . Это сделано из соображений экономии: известно, что эта связка является производной – она выражается через остальные. Желающие работать с ней, должны ввести ещё следующие две схемы аксиом:
Группа аксиом эквивалентности:
(Э1): ((A « B) ® ((A ® B) Ù (B ® A)))
(Э2): (((A ® B) Ù (B ® A)) ® (A « B))
Единственным правилом выводав формальном исчислении высказываний является уже знакомое правило Modus ponens (MP): 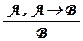 .
.
Доказательством формулы Вв формальной теории исчисления высказываний называется конечная последовательность формул В1 , … , Вn , где Вn совпадает с В, а каждая формула Bi (1 £ i £ n) либо является аксиомой, либо получена из предыдущих формул Вj и Вk (1 £ 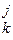 < i) по правилу Modus ponens, т.е. Вk = (Bj ® Bi) и применение правила (MP) таково:
< i) по правилу Modus ponens, т.е. Вk = (Bj ® Bi) и применение правила (MP) таково: 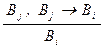 . Это значит, что из доказуемости формул Bj и Bj ® Bi постулируется возможность сделать вывод о доказуемости формулы Bi . Это далеко не очевидный логический ход, хотя многих птешит иллюзия, что он согласуется со здравым смыслом.
. Это значит, что из доказуемости формул Bj и Bj ® Bi постулируется возможность сделать вывод о доказуемости формулы Bi . Это далеко не очевидный логический ход, хотя многих птешит иллюзия, что он согласуется со здравым смыслом.
Формула В, для которой существует доказательство, называется доказуемой в формальном исчислении высказываний. В этом случае будем писать  В . В частности, всякая аксиома А доказуема, т.к. её доказательством является последовательность формул, состоящая из единственной формулы А.
В . В частности, всякая аксиома А доказуема, т.к. её доказательством является последовательность формул, состоящая из единственной формулы А.
Дата добавления: 2021-12-14; просмотров: 753;











