Примеры доказательств в формальном исчислении предикатов
1.  (" x P(x)) ® ($ x P(x))
(" x P(x)) ® ($ x P(x))
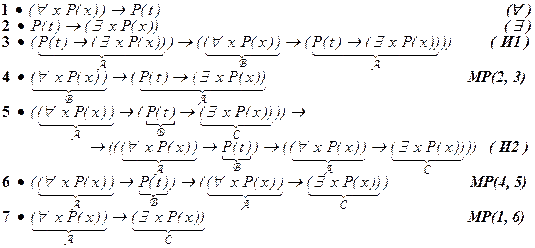
2. Анализ приведённого доказательства показывает, что аналогично можно обосновать правило вывода 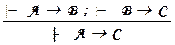 (правило силлогизма), которое можно использовать в дальнейшем. Обоснование следует доказательству примера 1.
(правило силлогизма), которое можно использовать в дальнейшем. Обоснование следует доказательству примера 1.
1 · A ® B (дано)
2 · B ® C (дано)
3 · (B ® C) ® (A ® (B ® C)) (И1)
4 · (A ® (B ® C)) MP(2, 3)
5 · (A ® (B ® C)) ® ((A ® B) ® (A ® C)) (И2)
6 · (A ® B) ® (A ® C) МР(4, 5)
7 · A ® C МР(1, 6)
3.  (" x P(x)) ® (" y P(y))
(" x P(x)) ® (" y P(y))
1 · (" x P(x)) ® P(y) (")
2 · (" x P(x)) ® (" y P(y)) (В")(1)
4.  (" x (" y P(x, y))) ® (" y (" x P(x, y)))
(" x (" y P(x, y))) ® (" y (" x P(x, y)))
1 · (" x (" y P(x, y))) ® (" y P(u, y)) (")
2 · (" y P(u, y)) ® P(u, v) (")
3· (" x (" y P(x, y))) ® P(u, v) силлогизм(1, 2)
4 · (" x (" y P(x, y))) ® (" u P(u, v)) (В")
5 · (" u P(u, v)) ® (" x P(x, v))(пример 3)
6 · (" x (" y P(x, y))) ® (" x P(x, v))силлогизм(4, 5)
7 · (" x P(x, v)) ® (" v (" x P(x, v)))(В")
8 · (" x (" y P(x, y))) ® (" v (" x P(x, v)))силлогизм(6, 7)
9 · (" v (" x P(x, v))) ® (" y (" x P(x, y)))(пример 3)
10 · (" x (" y P(x, y))) ® (" y (" x P(x, y)))силлогизм(8, 9)
III. Специальные формальные теории.Теория предикатов создавалась, чтобы дать возможность любой конкретной науке формулировать свойства изучаемых объектов на общем логическом языке и доказывать свои теоремы едиными средствами. Поэтому теория предикатов является неотъемлемой частью любой содержательной математической теории.
Вместе с тем, в каждой специальной математической теории рассматриваются свои, специфические предикаты, функции, объекты особого назначения и формулируются аксиомы, постулирующие свойства этих объектов, предикатов и функций. Специальная теория не имеет специфических правил вывода, а пользуется только правилами вывода теории предикатов.
Более формально, алфавит специальной теориисостоит из нескольких групп символов:
· достаточно большое количество переменных x, y, … , x100 , … для обозначения объектов теории,
· символы выделенных элементов c, d, … , c129 , … – константы– для обозначения объектов особого назначения,
· функциональные символы f 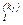 , … , f
, … , f 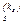 , …для обозначения специфических операций и функций, используемых в аксиомах специальной теории,
, …для обозначения специфических операций и функций, используемых в аксиомах специальной теории,
· предикатные символы P 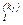 , … , P
, … , P 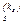 , … для обозначения специфических предикатов, используемых в аксиомах специальной теории,
, … для обозначения специфических предикатов, используемых в аксиомах специальной теории,
·Ù , Ú , ® , « , 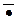 – логические связки,
– логические связки,
·", $– кванторы,
·служебные символы – ( , ) – скобки и , – запятая.
Понятие формулы специальной теории несколько усложняется из-за наличия функциональных символов. Вначале от простого к сложному вводится понятие терма (функционального выражения специальной теории) :
(Т1): любая объектная переменная является термом.
(Т2): любая константа (символ выделенного элемента) является термом.
(Т3): если t1 , … , tm – термы, а f (m) – один из функциональных символов теории, то f (m)(t1 , … , tm) – терм.
(Т4): других термов нет.
Теперь от простого к сложному строится понятие формулы специальной теории:
(Ф1): если t1 , … , tm – термы, а P (m) – один из предикатных символов теории, то P (m)(t1 , … , tm) – бескванторная формула, зависящая от всех переменных, участвующих в термах t1 , … , tm , причём все её переменные свободны.
(Ф2): если A и В – две формулы, то (A Ù B), (A Ú B), (A ® B), (A « B), 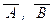 – тоже формулы, в которых свободны все вхождения объектных переменных, свободные в А или в В, и связаны все вхождения объектных переменных, связанные в А или в В.
– тоже формулы, в которых свободны все вхождения объектных переменных, свободные в А или в В, и связаны все вхождения объектных переменных, связанные в А или в В.
(Ф3): если A(x) – формула хотя бы с одним свободным вхождением объектной переменнойx, то выражения (" x A(x)) и ($ x A(x)) – формулы, в которых связаны вхождения всех объектных переменных, связанных в А, а также все вхождения x, и свободны все вхождения объектных переменных, свободные в А, кроме переменной х. При этом формула A(x) называется областью действия квантора.
(Ф4): других формул нет.
Система аксиом специальной теориисостоит из
· аксиом формального исчисления предикатов,
· специальных аксиом теории.
При этом, как правило, явно формулируются только специальные аксиомы, а аксиомами исчисления предикатов пользуются без лишних оговорок.
Правила вывода специальной теории, понятиядоказательства формулыи доказуемой формулыте же, что и в формальной теории предикатов.
IV. Пример специальной теории: формальная арифметика. Алфавитсостоитиз нескольких групп символов:
·достаточно большое количество переменных x, y, … , x100 , … для обозначения натуральных чисел,
·1 – выделенный элемент,
· + , × – знаки бинарных арифметических операций сложения и умножения,
· = – единственный предикатный символ равенства чисел,
·Ù , Ú , ® , « , 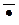 – логические связки,
– логические связки,
·", $– кванторы,
·( , ) – служебные символы (скобки).
Термы формальной арифметики – это просто арифметические выражения, которые строятся от простого к сложному так:
(АВ1): любая переменная является арифметическим выражением.
(АВ2): 1 – арифметическое выражение.
(АВ2): если A и В – арифметические выражения, то (А + В) и (А×В) – тоже арифметические выражения.
(АВ3): других арифметических выражений нет.
Примеры: 1.1 + x – не арифметическое выражение, т.к. нет скобок.
2. ((x + 1)×(z + t)) – арифметическое выражение.
Формулы арифметикитожеопределяются от простого к сложному:
(Ф1): если А, В – два арифметических выражения, то (А = В) – бескванторная формула, зависящая от всех переменных, участвующих как в А, так и в В, причём все её переменные свободны.
(Ф2): если A и В – две формулы, то (A Ù B), (A Ú B), (A ® B), (A « B), 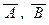 – тоже формулы, в которых свободны все вхождения объектных переменных, свободные в А или в В, и связаны все вхождения объектных переменных, связанные в А или в В.
– тоже формулы, в которых свободны все вхождения объектных переменных, свободные в А или в В, и связаны все вхождения объектных переменных, связанные в А или в В.
(Ф3): если A(x) – формула хотя бы с одним свободным вхождением объектной переменнойx, то выражения (" x A(x)) и ($ x A(x)) – формулы, в которых связаны вхождения всех объектных переменных, связанных в А, а также все вхождения x, и свободны все вхождения объектных переменных, свободные в А, кроме переменной х. При этом формула A(x) называется областью действия квантора.
(Ф4): других формул нет.
Примеры: 1. ((x = 1) Ù (y×x+1 = 1)) – бескванторная формула со свободными переменными x и y.
2. ((x + 1)×(z + t) + 1) = (t) – не формула (лишние скобки в правой части).
3. (" t ((x + 1)×(z + t) + 1) = (t + x + 1)) – формула с квантором, связывающим переменную t и свободными переменными x, z.
Аксиомы формальной арифметикикроме аксиом исчисления предикатов включают несколько групп аксиом:
Аксиомы равенства:
Рефлексивность: (" x (x = x))
Симметричность: (" x (" y ((x = y) ® (y = x)))
Транзитивность: (" x (" y (" z (((x = y) Ù (y = z)) ® (x = z))))
Схема подстановки: для любых арифметических выражений А, В, С с выделенным вхождением выражения В в А (символически А = А(В)) следующая формула является аксиомой ((В = С ) ® (А(В) = А(С))), где А(С) – результат замены выделенного вхождения подвыражения В в А на С .
Это – очень сильная форма подстановки, её можно значительно ослабить.
Условимся для арифметических выражений А(x1 , … , xn) и В(y1 , … , ym) использовать краткую запись А(x1 , … , xn) ¹ В(y1 , … , ym) вместо отрицания 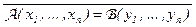 .
.
Аксиомы операций сложения и умножения:
Существование и единственность следующего: (" x ($ ! y (y = x + 1)))
Единица – наименьший элемент: (" x ((x + 1) ¹ 1))
Равенство следующих: (" x (" y ((x + 1) = (y + 1)) « (x = y)))
Ассоциативность прибавления 1: (" x (" y ((x + (y + 1)) = ((x + y) + 1))))
Единица – нейтральна по умножению: (" x ((x×1) = x))
Связь сложения и умножения: (" x (" y ((x×(y + 1) = ((x×y) + x)))))
Схема формальной индукции
Для любой формулы арифметики А(x) со свободной переменной x следующая формула является аксиомой: ((А(1) Ù (" y (А(y) ® А(y + 1)))) ® (" x А(x))).
Правила вывода формальной арифметики, понятиядоказательства формулыи доказуемой формулыв формальной арифметике такие же, как в формальном исчислении предикатов.
Дата добавления: 2021-12-14; просмотров: 310;











