Основные уравнения и векторные диаграммы
Если ко вторичной обмотке присоединить нагрузку zH, то в обмотке и в нагрузке появится ток I2, а на нагрузке — падение напряжения U2, которое называют напряжением вторичной обмотки (рис. 2.7). Возрастет при этом и ток первичной обмотки.
Действующие значения напряжений и токов трансформаторов регламентируют. Наибольшие длительно допустимые напряжения для данного трансформатора называют соответственно номинальным напряжением первичной обмотки и номинальным напряжением вторичной обмотки и обозначают: U1H, U2H. Наибольшие длительно допустимые токи обмоток также называют номинальными токами первичной и вторичной обмоток и обозначают: I1н, I2н. Величины номинальных напряжений и токов указываются в паспорте трансформатора, наряду с его номинальными мощностью, КПД, коэффициентом мощности и другими параметрами.
При наличии токов в первичной и вторичной обмотках они создают потоки рассеяния Фσ1 и Фσ2 которые замыкаются, в основном, по воздуху (рис. 2.7), и наводят в соответствующих обмотках ЭДС рассеяния:
eσi = - Lσ1di1/dt; eσ2= - Lσ2di2/dt,
где Lσ1 и Lσ2 — индуктивности рассеяния первичной и вторичной обмоток; i1 и i2 — токи первичной и вторичной обмоток. Действующие значения ЭДС рассеяния:
Eσ1 = ωLσ1I1 =X1I1 Eσ2 = ωLσ2I2=X2I2 ,(2.12)
где X1 =ωLσ1 и Х2=ωLσ2 — индуктивные сопротивления рассеяния первичной и вторичной обмоток.
Поскольку токи и напряжения первичной и вторичной обмоток могут по величине сильно отличаться друг от друга, то для удобства построения векторных диаграмм и анализа процессов осуществляют приведение вторичной обмотки к первичной так, чтобы ЭДС первичной и приведенной вторичной обмоток были бы равны Е1=E’2. При этом должны остаться неизменными мощность трансформатора, его КПД, коэффициент мощности.
Приведение параметров вторичной обмотки к первичной используется для удобства анализа и расчета трансформаторов и сводится к умножению или делению неприведенных величин на коэффициент трансформации k.
U΄2 = kU2; E΄2= kE2 I΄2 = I2 /k. (2.13)
Приведенные активное и индуктивное сопротивления вторичной обмотки получают умножением значений R2 и Х2 на k2:
R΄2 = k2R2; Х΄2 = k2X2 (2.14)
Для первичной и вторичной обмоток в соответствии со вторым законом Кирхгофа справедливо уравнение:
Ūl=-Ē1+Ī1 R1+jĪ1X1
(2.15)
Ū΄2 = Ē΄2+Ī΄2 R΄2+jĪ΄2X΄2,
где Ū1, Ū΄2 — векторы первичного и приведенного вторичного напряжений; Ē1, Ē΄2 — соответствующие ЭДС; Ī1, Ī΄2 — векторы тока первичной обмотки и приведенный ток вторичной обмотки; R1 R΄2 — активные сопротивления первичной и приведенное вторичной обмоток; Х1 Х'2 — индуктивные сопротивления первичной и приведенное вторичной обмоток.
В режиме холостого хода магнитный поток создается лишь магнитодвижущей силой (МДС) первичной обмотки. Его амплитудное значение:
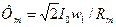 (2.16)
(2.16)
где Rm — магнитное сопротивление магнитопровода магнитному потоку Фm.
При работе трансформатора под нагрузкой основной магнитный поток создается совместным действием МДС первичной и вторичной обмоток:
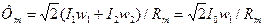 (2.17)
(2.17)
откуда в векторной форме получим:
Ī0w1 = Ī1w1+Ī2w2.
Разделим обе части уравнения на w,l,
Ī0 = Ī1+ Ī2w2 /w1
Ī0 = Ī1+Ī’2 или Ī1= Ī0+ (-Ī’2); (2.18)
Последнее уравнение показывает, что ток первичной обмотки Ī1, представляет собой сумму токов, из которых одна Ī0 создает МДС Ī0w1 необходимую для наведения в магнитопроводе основного магнитного потока Фm, а другая Ī2 создает Последнее уравнение показывает, что ток первичной обмотки Ī1, представляет собой сумму токов, из которых одна Ī0 создает МДС Ī0w1 необходимую для наведения в магнитопроводе основного магнитного потока Фm, а другая Ī΄2 создает МДС Ī΄2w1, которая компенсирует размагничивающее действие МДС вторичной обмотки Ī2w2.
Таким образом, любое изменение тока нагрузки Ī2 влечет изменение тока Ī1 первичной обмотки.
Поскольку 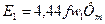 , a U1 ≈ Е1, то
, a U1 ≈ Е1, то 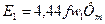 , следовательно:
, следовательно:
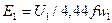 (2.19)
(2.19)
Из (2.19) следует, что основной магнитный поток не зависит от нагрузки трансформатора, а является функцией напряжения на первичной обмотке и его частоты.
На основании (2.15) и (2.18), которые называют основными уравнениями трансформатора, построим векторные диаграммы трансформатора в режиме активно-индуктивной и активно-емкостной нагрузки.
Векторная диаграмма нагруженного трансформатора при активно-индуктивной нагрузки представлена на рис. 2.10,a.
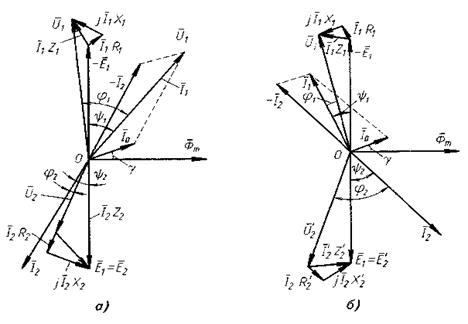
|
Рис. 2.10. Векторная диаграмма трансформатора при активно-индуктивной (а) и активно-емкостной (б) нагрузке
Построение диаграммы начнем с вектора основного магнитного потока Фm. Вектор тока I0 опережает по фазе поток Фm на угол магнитного запаздывания γ. Так учитывают электрические и магнитные потери в цепи намагничивания. Магнитный поток Фm, проходя по сердечнику, индуктирует в первичной обмотке ЭДС Ē΄1 во вторичной обмотке Ē΄2, которые отстают от потока на 90°. Рассмотрим случай активно-индуктивной нагрузки трансформатора. При такой нагрузке ток вторичной обмотки Ī΄2 отстает от Ē΄2 на угол ψ2. Вычитая из вектора Ē΄2 векторы активного Ī΄2R΄2 и индуктивного Ī΄2Х΄2 падений напряжения во вторичной обмотке, получим вектор вторичного напряжения Ū΄2, который опережает ток Ī΄2, на величину угла φ2.
Для получения вектора тока в первичной обмотке Ī1 воспользуемся уравнением токов (2.18).
Откладывая вектор Ī΄2 в обратном направлении и складывая его с вектором Ī0, получим вектор Ī1. Для получения напряжения Ū1 первичной обмотки трансформатора применим уравнение напряжений (2.15). Отложив вектор Ē΄1 и складывая его с вектором активного Ī1R1 и индуктивного Ī1Х1 и падений напряжений в первичной обмотке, получим вектор Ū1. Суммарное падение напряжения соответствует Ī1Z1.
Напряжение первичной обмотки U1 опережает ее ток Ī1 на угол φ1. Физически это означает, что трансформатор потребляет из сети и активную, и реактивную мощности, которые идут на покрытие электрических и магнитных потерь в трансформаторе, и, главным образом, обеспечивают активной и реактивной мощностью присоединенную к трансформатору активно-индуктивную нагрузку.
Из векторной диаграммы видно, что увеличение нагрузки трансформатора приводит к увеличению тока Ī΄2, а это вызывает в свою очередь увеличение тока Ī1 потребляемого трансформатором из сети.
При активно-емкостной нагрузке трансформатора ток вторичной обмотки Ī'2 опережает Ē΄2 на угол ψ2 (рис. 2.10,б). Вычитая из вектора Ē΄2 векторы активного Ī΄2R΄2 и индуктивного Ī΄2Х΄2 падений напряжения во вторичной обмотке, получим вектор вторичного напряжения Ū΄2, который отстает от тока Ī΄2 на величину угла φ2. Соответственно ток первичной обмотки Ī1, опережает напряжение U1 на угол φ1. Это означает, что трансформатор получает из сети активную мощность, а в сеть отдает избыточную реактивную мощность, которая генерируется в цепи вторичной обмотки присоединенными к ней конденсатора.
Дата добавления: 2021-12-14; просмотров: 524;











