Параллельность прямой и плоскости.

Прямая и плоскость параллельны, если они не имеют общих точек.

Теорема: Если плоскость β проходит через прямую a , параллельную плоскости α, и пересекает эту плоскость по прямой b , то b//а

Доказательство: самостоятельно.

Прямую b иногда называют следом плоскости β на плоскости α.

Теорема: Прямая, параллельная плоскости, параллельна бесчисленному множеству прямых, лежащих в этой плоскости и параллельных между собой.

Доказательство:

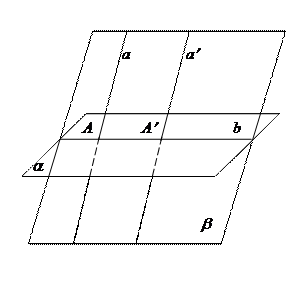
Через точку АÎa и прямую а проведем плоскость p, которая пересечет a по прямой а¢. по предыдущей теореме прямая а¢//а. В плоскости a бесконечно много прямых, параллельных прямой а¢. Все они параллельны между собой и параллельны прямой а.

Замечание: Все остальные прямые плоскости a не параллельны прямой а, т.к. не параллельны а¢. Поэтому заменить в формулировке слова «бесчисленному множеству прямых» на «всем прямым» нельзя!

Теорема: Если одна из двух параллельных прямых пересекает некоторую плоскость, то и другая прямая также пересекает эту плоскость.

Доказательство:

Проведем плоскость b через а и а¢. Плоскость b с плоскостью a имеют общую точку А, следовательно они имеют общую прямую b. Прямая bÎb и пересекает прямую а, а значит пересекает и прямую а¢ в некоторой точке А¢. Но с другой стороны bÎa, и т.к. А¢Îb, то А¢Îa, и значит а¢ и a имеют общую точку, т.е. а¢ пересекает a.