Параллельность плоскостей.

Теорема: Плоскость, параллельнаядругой плоскости параллельна всем прямым этой плоскости.

Доказательство (от противного): Пусть a//b и аÎb. Докажем, что а//a. Если ане параллельна плоскости a, то она либо

1) лежит в данной плоскости, что противоречит условию a//b либо

2) пересекает плоскость a, тогда плоскости a и bимеют общую точку, т.е. пересекаются, что также противоречит условию a//b

Значит любая прямая плоскости b параллельна плоскости a

Теорема: (признак параллельности плоскостей) Если две пересекающиеся прямые одной плоскости соответственно параллельны двум пересекающимся прямым второй плоскости, то плоскости параллельны

Доказательство: самостоятельно

Теорема: Через точку, лежащую вне плоскости, проходит плоскость параллельная данной и притом только одна.

Доказательство: Пусть аÎa, а¢Îa и прямые а и а¢ не параллельны. Через точку А 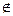a проведем две прямые АХ и АХ¢ так, чтобы АХ//а и АХ¢//а¢.

Тогда плоскость АХХ¢ будет параллельна плоскости a.

Всякая плоскость, параллельна плоскости a, и проходящая через точку А, должна совпасть с плоскостью АХХ¢ (почему?

)

Теорема: две плоскости, параллельные третьей, параллельны между собой.

Доказательство: самостоятельно