Передаточное отношение ступенчатого ряда колёс

(рис. 2.13)

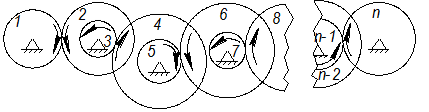
Этот ряд отличается тем, что колёса на осях помещаются блоками, то есть

Рис. 2.13

на каждой оси закреплено по два колеса число колёс в этом ряду всегда четное. Применяя все выкладки как для последовательного ряда, можно сделать вывод, что передаточное отношение равно произведению передаточных отношений отдельных ступеней этого ряда.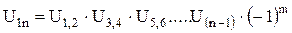

Этот ряд применяется для получения большого передаточного отношения или для значительного увеличения (уменьшения) момента.

2.3. Передаточное отношение планетарных и дифференциальных механизмов

(рис. 2.14)

Звенья, вращающиеся вокруг неподвижной оси, называются основными или центральными.

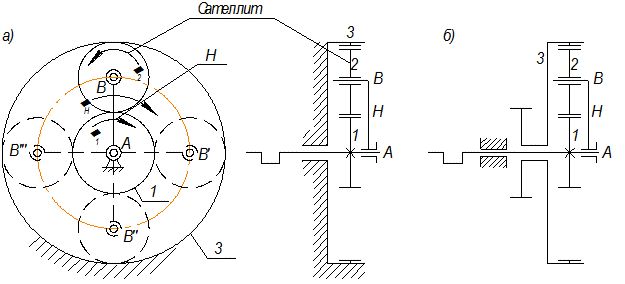
Центральное колесо 1 называется солнечным, а неподвижное 3 - коронным или корончатым. Зубчатое колесо 2 имеющее подвижную ось называется сателлитом. Звено Н называется водилом или поводком. Механизмы, в состав которых входят зубчатые колеса с подвижными осями называются планетарными или дифференциальными.

Планетарными (рис. 2.14 а) называются механизмы, имеющие одну степень свободы. Дифференциальные (рис. 2.14 б) механизмы имеют две и более степени свободы.

Рис. 2.14

Эти механизмы обязательно должны быть соосными, то есть оси солнечных колёс должны располагаться на одной и той же прямой линии.

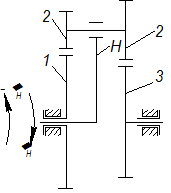
Рассмотрим дифференциальный механизм (рис. 2.15).

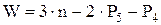
где: n=4; ; .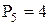

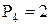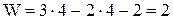, таким образом определённость в движении звеньев этого механизма будет в том случае, если будут известны законы движения двух его ведущих звеньев.

Так как сателлиты имеют подвижные оси, то использовать формулы для расчёта передаточного отношения механизмов с неподвижными осями не представляется возможным. В этом случае прибегают к методу инверсии (метод обращённого движения).

Будем рассматривать движение всех колёс относительно водила. Всем звеньям зададим вращательное движение с угловой скоростью 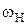водила, но в обратном направлении 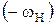и найдём скорости всех звеньев механизма. Для этого вычтем угловую скорость водила из всех угловых скоростей колёс.

Рис. 2.15

Таблица 2.

№ Звеньев	Скорость звена в действительном движении (до инверсии)	Скорость звена в обращённом движении (после инверсии)
Колесо 1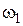
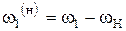
Колесо 2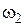
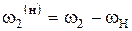
Колесо 2’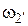
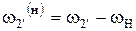
Колесо 3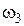
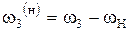
Звено Н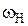

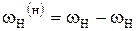
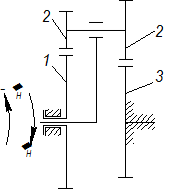
Механизм, полученный в результате инверсии (остановки водила) называется обращённым (рис. 2.16). В результате получили обычную зубчатую передачу с неподвижными осями.

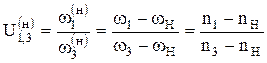
(2.1)

Эту зависимость (2.1) называют формулой Виллиса для дифференциальных механизмов.

Если бы было n - колёс, то:

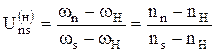
где s – солнечное колесо.

Дифференциальный механизм никакого определённого передаточного отношения не имеет, если ведущим является одно из звеньев (колесо или водило), и приобретает определённость, если ведущих колёс будет два.

Рис. 2.16

Передаточное отношение 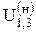обращённого механизма можно рассчитать,

зная числа зубьев колёс.

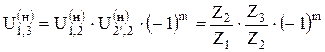
У планетарных механизмов (рис. 2.16) одно из центральных (основных) колёс неподвижно, тогда формула Виллиса примет вид:

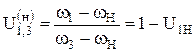
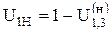
или в общем случае: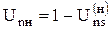

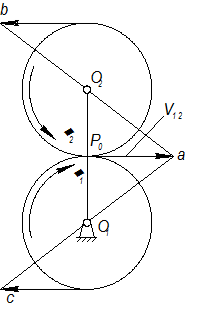
Рис. 2.17

Передаточное отношение планетарного механизма от любого n-го колеса равно 1 минус передаточное отношение от этого же самого колеса к солнечному колесу, при неподвижном водиле.