Кинематический анализ кулачковых механизмов методом диаграмм

Рассмотрим некоторую типовую функцию положения толкателя заданную графически .

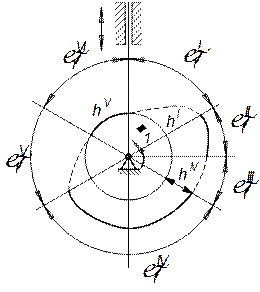
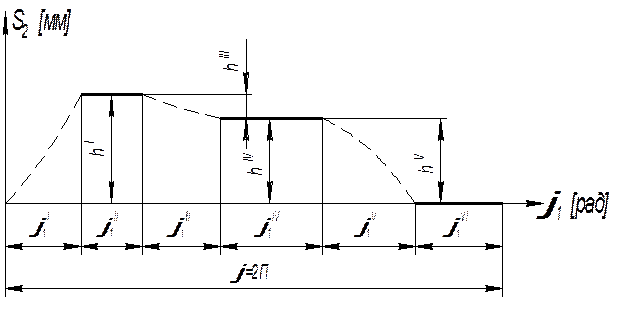
Рис. 2.1

Пусть угол поворота кулачка 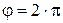соответствует полному циклу движения механизма. На угле происходит подъем толкателя на величину .

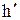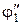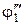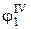Далее, на угле поворота толкатель имеет выстой. На угле поворота происходит опускание толкателя на величину . На угле поворота толкатель имеет второй выстой. На угле поворота 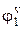он опускается на величину 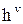, и на угле 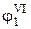толкатель имеет вновь выстой.

Углы , , 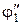, 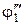…носят название фазовых углов. Участки кривой соответствующие фазовым углам называются фазой подъемы, фазами выстоя, фазой опускания.

Нетрудно видеть, что в углах , , 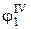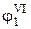соответствующих фазам выстоя, профиль кулачка должен быть очерчен по дугам окружностей с радиусами ;

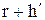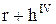и к, где к – наименьший радиус кулачка.

На рисунке был рассмотрен кулачковый механизм с поступательно движущимся звеном, не все определения и положения применимы и для кулачковых механизмов с коромыслом. В этих случаях диаграмма движения задается в виде функции .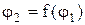

Рассмотрим несколько диаграмм аналогов ускорений, определяющих законы движения ведомых звеньев.

На (рис. 2.2) показана диаграмма аналога постоянного ускорения. Соответственно (рис. 2.3) аналог скорости пути. Представленный этими диаграммами закон определяет равноускоренное движение ведомого звена.

Диаграмма аналога ускорения имеет разрывы, определяющие мягкий удар. Для быстроходных механизмов такой закон неприемлем из-за больших сил инерции толкателя как коромысла.

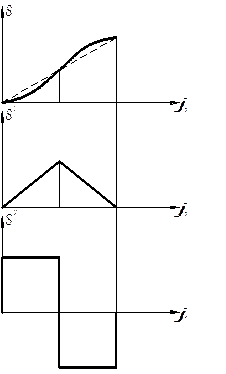
Рис. 2.2

При скачкообразном изменении диаграммы аналога ускорений толкатель получает мягкий удар, происходящий из-за резкого изменения динамических нагрузок, вызывающих упругие колебания.

Избежать скачки ускорений (рис. 4) можно при треугольной диаграмме аналогов ускорения.

Диаграмма аналога ускорения, (рис. 2.5) показывает, что в середине движения нет скачка ускорения, но в начале и в конце движения имеются.

Рис.2.49

Удачным законом движения считается трапецеидальный (рис. 2.6)

Значительное распространение получили диаграммы аналогов ускорения, изменяющихся по законам тригонометрических функций.

Ускорение, изменяющееся по косинусоидальному закону, вызывает мягкий удар (рис. 2.7) При синусоидальном законе ударов нет.

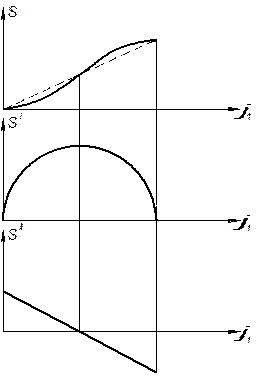
Рис. 2.3	Рис. 2.4

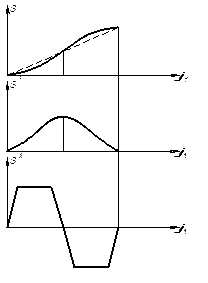
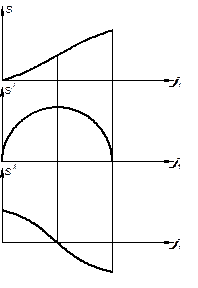
Рис. 2.5	Рис. 2.6	Рис. 2.7