Модуль упругости. Коэффициент Пуассона

Вопрос об определении нормальных напряжений теснейшим об­разом связан с расчетами бруса на прочность. Умение вычислять деформации и перемещения необходимо для расчетов на жесткость, а также для определения сил в статически неопределимых системах.

Выделим из бруса, изображенного на рис. 17.7 бесконечно малый элемент длиной dz.

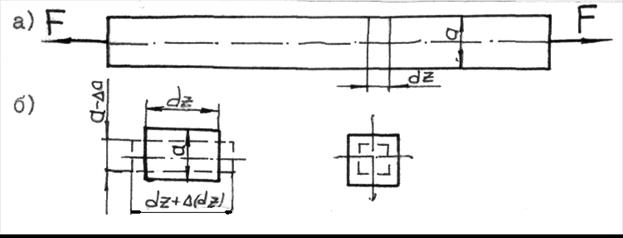
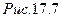
Отношение приращения (изменения) длины элемента к его первоначальной длине называется относительным удлинением или продольной деформацией:

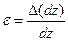(17.2)

Очевидно, продольная деформация – безразмерная величина. В некоторых случаях ее выражают в процентах. При растяжении продольную деформацию считают положительной, а при сжатии – отри­цательной.

Отношение изменения 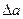размера поперечного сечения к его первоначальному значению называют относительным поперечным сужением (расширением), или поперечной деформацией:

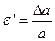(17.3)

Продольную и поперечную деформации называют также линейными деформациями.

В известных пределах нагружения между 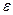(деформацией) и соответствующим (действующим в ее направлении) 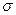напряжением существует прямо пропорциональная (линейная) зависимость.

Это положение носит название закона Гука и записывается в виде

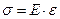(17.4)

Коэффициент пропорциональности E называют модулем продольной упругости (модуль упругости 1-го рода; модуль Юнга). Е имеет ту же размерность, что и напряжение, т.е. выражается в Па или МПа.

Модуль продольной упругости – физическая постоянная данного материала, характеризующая его жесткость. Чем жестче материал, тем меньше он деформируется при данном напряжении.

Опытным путем установлено, что при простом растяжении или сжатии отношение поперечной деформации к продольной – величина постоянная для данного материала. Это отношение, взятое по абсолютному значению, называется коэффициентом поперечной деформации, или коэффициентом Пуассона;

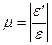(17.5)

Значения коэффициента Пуассона для различных материалов находятся в пределах от 0 до 0.5.

Минимальное значение коэффициент Пуассона имеет для пробки ( 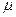= 0); максимальное – для каучука ( 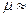0.5). Для большинства металлов и сплавов значение коэффициента Пуассона колеблется в сравнительно узких пределах: от 0.23 до 0.35 (в среднем примерно 0.3).

Вопрос об определении изменения длины (удлинения или укорочения) бруса. Удлинение или укорочение равно:

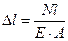(17.6)

Выражение (17.6) часто называют формулой Гука, а произведение Е∙А условно называют жесткостью сечения бруса при растяжении (сжатии).

Понятие жесткости бруса (участка бруса)определяется по формуле

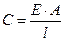(17.7)

Жесткость бруса численно равна силе, вызывающей удлинение (или укорочение) бруса, равное единице длины: 1 м или 1 см и т.п.

При расчетах в единицах СИ коэффициент жесткости выражают в ньютонах на метр (Н/м).

Величину, обратную коэффициенту жесткости, называют коэффициентом податливости:

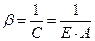(17.8)

Коэффициент податливости численно равен удлинению (укорочению) бруса, вызванному силой, равной единице силы: 1 H или 1 кН.

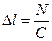(17.9)

или

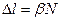(17.10)

17.4. Частный случай плоского напряженного состояния – чистый сдвиг.
Закон Гука при сдвиге.

Рассмотрим частный случай плоскогонапряженного состояния, для которого отличные от нуля главные напряжения равны по модулю и противоположны по знаку (рис. 17.8).

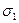Такое напряженное состояние носит название чистого сдвига. Максимальное главное напряжение следует обозначить , минимальное 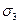; по условию, 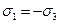; промежуточное главное напряжение 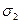= 0.

Чистым сдвигом называют такое плоское напряженное состоя­ние, при котором в окрестности данной точки можно выделить элемент таким образом, чтобы на четы­рех его гранях были только равные между собой касательные напряжения.

В качестве примера, иллюст­рирующего возникновение чистого сдвига, рассмотрим кручение тонко­стенной трубы (рис. 17.9 а). Из условия равновесия отсеченной части трубы, изображенной отдельно на рис. 17.9 б, следует, что в поперечном сечении (любом) возни­кает лишь один внутренний силовой фактор – крутящий момент 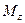, численно равный

внешнему моменту М. В поперечном сечении трубы возникают касательные напряжения ( ).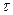

Деформация сдвига. Изобразим элемент, выделенный площадками, на которых возникают только касательные напряжения. Учитывая, что нас интересуют деформации элемента, а не его перемещения как твер­дого тела, будем считать одну из граней неподвижной. Мерой деформации сдвига служит изменение первоначального прямого угла между гранями элемента, называемое углом сдвига и обозначаемое 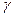. Угол сдвига, выражается в радианах (рис. 17.10).

Между углом сдвига и соответствующим касательным напряжением существует прямая пропорциональность – закон Гука при сдвиге.

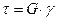(17.11)

Здесь G – упругая постоянная материала, характеризующая его жесткость при деформации сдвига и называемая модулем сдвига или модулем упругости 2-го рода. Размерность модуля сдвига та же, что и напряжения.

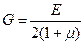(17.12)