Напряжение как мера внутренних сил

Для суждения об интенсивности внутренних сил в определен­ной точке данного сечения введено понятие о напряжении.

Выделим в окрестности интересующей нас точки сечения малую площадку пло­щадью 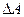; допустим, что на этой площад­ке возникает внутренняя сила 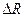(рис. 16.5) Отношение этой внутренней силы к площади выделенной площадки называется средним напряжением 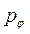в окрестности рассматриваемой точки по проведенному сечению (на площадке ):

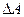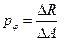(16.2)

Истинное напряжение в данной точке рассматриваемого сече­ния:

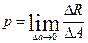(16.3)

Отношение будет величиной конечной.

Напряжение в данной точке по рассматриваемому сечению есть величина векторная (вектор 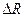делим на скаляр 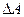); направление этого вектора совпадает с предельным направлением вектора .

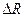Единица измерения напряжения – Паскаль (Па).

Паскаль – это напряжение, при кото­ром на площадке в 1 м² возникает внут­ренняя сила, равная 1 H, но эта единица, очень мала, поэтому используется кратная ей единица – мегапаскаль, 1 МПа = 10⁶ Па.

Разложим вектор напряжения р на две составляющие: одну – направленную по нор­мали к сечению (нормальное напряжение 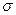), вторую – лежащую в плоскости сечения (ка­сательное напряжение 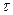) (рис. 16.6). Между напряжениями р, 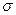и 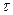су­ществует следующая очевидная зависимость:

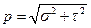(16.4)

В ряде случаев оказывается удобным разложить вектор р не на две, а на три составляющие, направленные параллельно коорди­натным осям. Правило индексов: первый индекс указывает, какой оси параллельна нормаль к площадке действия рассматриваемого напряжения, второй индекс показывает, какой оси параллельно данное напряжение.

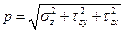^. (16.5)

Установим связь между напряжениями и внутренними силовыми факторами в поперечном сечении бруса. Элементарные внутренние силы:

; ; .

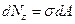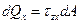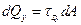Выражения составляющих главного вектора внутренних сил:

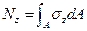; (16.6)

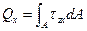; (16.7)

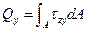. (16.8)

Умножая каждую из элементарных сил на расстояние до соответствующей оси, получаем элементарные моменты внутренних сил:

; ;

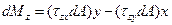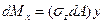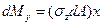
Суммируя элементарные моменты по всей площади сечения, получаем выражения для составляющих главного момента внутренних сил:

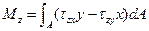; (16.9)

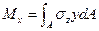; (16.10)

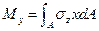. (16.11)

Выражения (16.6)–(16.11) не служат для вычисления внутренних силовых факторов. Они выражают физическую сущность внутренних силовых факторов.