С подвижными осями вращения

Зубчатая передача, у которой геометрическая ось хотя бы од­ного из колес подвижна, называется планетарной. Различные плане­тарные механизмы можно представить в виде трех типов передач.

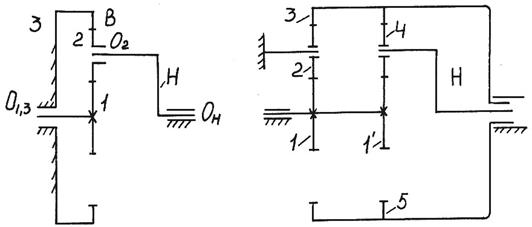
1. Простые планетарные передачи, обладающие одной степенью подвижности, у которых одно из основных звеньев закреплено непо­движно (рис. 15.7, закреплено звено 3). Такие механизмы служат для последовательной передачи потока мощности.

2. Дифференциальные передачи, обладающие двумя степенями подвижности, у которых все основные звенья подвижны (рис. 15.6). Эти передачи позволяют суммировать два или несколько потоков мощнос­ти, поступающих от независимых источников, либо распределять их по независимым потребителям.

3. Замкнутые дифференциальные передачи, получаемые из дифференциальных передач путем замыкания двух основных звеньев (центрального колеса и водила) простой передачей, состоящей из колес 1, 2, 3 (рис. 15.8). Такие передачи позволяют получить большие пе­редаточные отношения при малых габаритах.

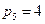Рассмотрим механизм, изображенный на рис. 15.6. Определим число степеней подвижности, если = 4 - число звеньев, и 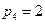– число кинематических пар V и IV класса.

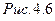
Определенность в движении звеньев уэтого механизма будет в том случае, если будут заданы законы движения двум звеньям.

Основными звеньями механизмов с подвижными осями являются водило (Н) и соосные с ним колеса (1 и 3). В данном случае все основные звенья подвижные. Оба эти признака (W> 1 и подвижные основные звенья) определяют дифференциальный механизм.

Определим степень подвижности для механизма, изображенного на
рис. 15.7

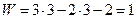
У этого механизма колесо 3 (основное звено) неподвижно и W= 1. Оба признака определяют планетарный механизм. Механизмы замкнутых

дифференциалов имеют все основные звенья подвижными, но число степеней подвижности равно единице (W= 1). Таким об­разом, только по совокупности двух признаков механизмы с подвиж­ными осями можно отнести к тому или иному типу.

Формулы 15.5, 15.7 для определения передаточного отношения планетарных и дифференциальных механизмов использовать нельзя, так как сателлит участвует в сложном движении, состоящем из вра­щения вокруг оси O₂ и вращения вместе с водилом Н вокруг оси О_н (см. рис.15.6, 15.7).

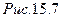
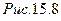
Для вывода зависимостей, связывающих угловые скорости меха­низмов, имеющих подвижные оси, воспользуемся методом обращения движения.

Допустим, что в действительном движении звенья механизма (см.рис.15.6) имеют угловые скорости . Сооб­щим всем звеньям скорость, равную угловой скорости водила, но противоположно ей направленную, т.е. 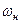. В этом случае угловые скорости звеньев будут соответственно равны:

Так как водило Н стало неподвижным ( ), то мы получили "обращенный механизм" с неподвижными осями. Для этого меха­низма справедлива зависимость

где 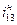–передаточное отношение "обращенного механизма, кото­рое можно определить через число зубьев колес:

В правую часть предыдущей зависимости подставим значение относительных скоростей:

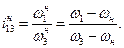(15.9)

Полученное уравнение называется формулой Виллиса для дифференциальных механизмов. Левая часть, как показано выше, может

быть выражена через число зубьев колес. Определенность в решении правой части будет иметь место, когда будут известны скорости двух ведущих звеньев. Установим, какой вид примет формула Вилли­са для планетарного механизма, изображенного на рис. 15.7. У этого механизма колесо 3 жестко соединено со стойкой (заторможено), т.е. .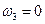

Таким образом, имеем

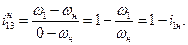
Откуда 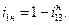(15.10)

Полученную зависимость называют формулой Виллиса для плане­тарных механизмов, а передаточное отношение – планетарным передаточным отношением.

Как и для дифференциальных механизмов, 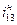определяется че­рез число зубьев колес.

В общем случае:

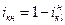
где 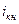– передаточное отношение от звена К к звену l (l – соответствует неподвижному центральному колесу).

Достоинством планетарных механизмов является возможность получения больших передаточных отношений при малых габаритах.

Пример 1. Определить передаточное отношение планетар­ного механизма (рис. 15.9), если Z₁ = 100, Z₂ = 99, Z_2´ = 100, Z_3´ = 101.

Это одноступенчатый планетарный редуктор. Используя формулу (15.10), запишем

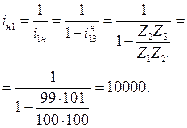
Пример 2. В зубчатой передаче, показанной на рис. 15.10, входное коническое колесо 1 в данный момент имеет угловую ско­рость 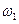= 340 с^-1 и постоянное угловое ускорение = 285 с^-2 , направленное по движению.

Z₁ = Z₂ = 18; Z_2´ = Z_4´ = 18; Z₃ = Z₅ = 30; Z_3´ = Z_5´ = 22; Z₄ = Z₆ = 70.

Принять средний модуль конического колеса m_m = 2 мм, шири­ну колеса b= 20 мм, плотность ρ = 8000 кг/м, смещение центра масс (точки А, рис.15.11) l = 2 мм.

Определить:

1) передаточное отношение между входным и выходным звеньями и направление вращения;

2) угловую скорость и угловое ускорение выходного звена, их направление показать на схеме передачи;

3) время, в течение которого угловая скорость увеличится в 2 раза;

4) величину и направление силы инерции и момента пары сил инерции звена 1 в начале и в конце найденного в предшествующем пункте промежутка времени, сравнить силу инерции с силой тяжести и показать чертежом направления вращения, ускорения и инерцион­ных нагрузок;

5) общий коэффициент полезного действия передачи.

Решение.

1. Определить передаточное отношение механизма.

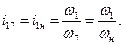
Выделим из механизма ступень с неподвижными осями, состоящую

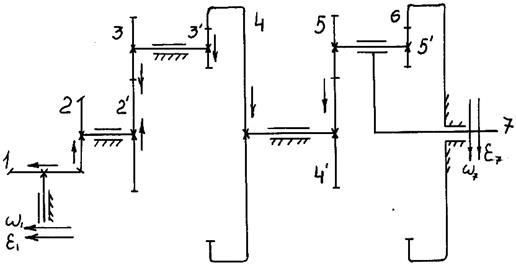
из колес Z₁, Z₂, Z_2´, Z₃, Z_3´, Z₄, и планетарную ступень, состоящую из колес Z_4´, Z₅, Z_5´, Z₆ и водила Н (7);

а) для ступени с неподвижными осями

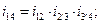
оси колес 1 и 4 непараллельные, поэтому знак передаточного отношения не определяем, а покажем направления вращения колес не­подвижной ступени в соответствии с правилом стрелок:

б) чтобы определить передаточное отношение планетарной ступени, используем формулу Виллиса; остановим водило Н (7), исполь­зуя зависимость (15.9), получим

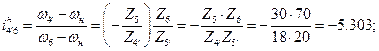
колесо 6 неподвижно ( 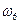= 0), используя зависимость (15.10), получим

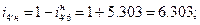
в) передаточное отношение всего механизма

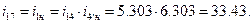
Передаточное отношение планетарной ступени 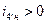. Сле­довательно, водило Н (7) вращается в ту же сторону, что и колесо 4.

Покажем направление угловой скорости и углового ускоре­ния 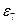на чертеже стрелками.

Поскольку , вращение ускоренное.

2. Угловая скорость и угловое ускорение ведомого звена 7 по модулю:

3. Определить время, в течение которого угловая скорость увеличивается вдвое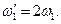

Для ускоренного вращения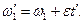

Отсюда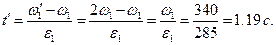

4. Для расчета момента инерции коническое ведущее ко­лесо со средним модулем m_m = 2 мм, Z₁ =18 заменим цилиндром с диаметром, равным среднему делительному диаметру.

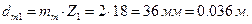
С учетом сказанного масса определяется по формуле

где ρ – плотность, ρ = 8000 кг/м³ (по условию).

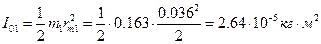
Вес колеса

Смещение центра масс (точки А) (см. рис. 15.11)

l = 2 мм = 0,002 м.

Нормальная составляющая силы инерции

Нормальное ускорение точки A.

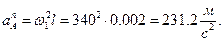
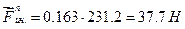
Касательное ускорение точки A и касательная составляющая силы инерции:

Определим полное ускорение точки А, силу инерции и направ­ление силы инерции:

В практических расчетах составляющей 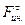как малой вели­чиной можно пренебречь и считать, что 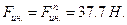Сравним силу тяжести и силу инерции:

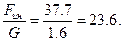
Силой веса по сравнению с силой инерции при практических расчетах такие можно пренебречь.

Момент сил инерции

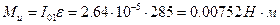
Покажем направление всех векторных величин на чертеже.

5. Определить общий КПД механизма.

Здесь – КПД конической пары с учетом потерь в подшипниках[4].

– КПД цилиндрической пары (2 пары по условию);

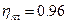– КПД планетарной передачи.