Третья форма уравнений равновесия.

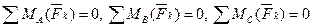
Если произвольная плоская система сил уравновешена, то алгебраические суммы моментов сил относительно любых трех точек, не лежащих на одной прямой, равны нулю.

Частные случаи решения этого уравнения:

1. К телу может быть приложена уравновешенная система параллельных сил, тогда, рационально расположив оси координат (например, ось X – перпендикулярно силам, а ось Y – параллельно им) получим

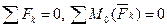
Если плоская система параллельных сил уравновешена, то алгебраическая сумма проекций сил на ось, параллельную силам, и алгебраическая сумма моментов сил относительно любой точки равны нулю.

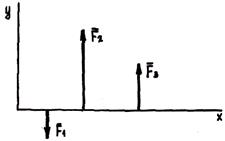
2. Расположив центры моментов A и В на прямой, перпендикулярной направлениям сил, получим

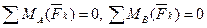
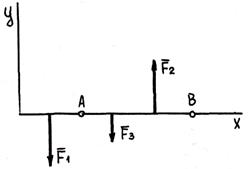
Если плоская система параллельных сил уравновешена, то равны нулю алгебраические суммы моментов сил относительно двух любых точек, лежащих на прямой, не параллельной линиям действия сил.

Для плоской системы параллельных сил получим два уравнения равновесия, т.е. для того, чтобы задача могла быть решенной, число неизвестных сил должно быть не больше двух. Вообще говоря, все задачи на равновесие системы сил, в которых число неизвестных не превосходит числа уравнений статики для этой системы, называются статически определимыми. Если же число неизвестных сил превышает число уравнений статики, которые возможно составить для данной системы, то задача называется статически неопределимой.