Загальні методи. Рішення задач оптимізації.

Система, для якої показник якості має екстремальне значення, називається оптимальною.

Параметри системи, при яких забезпечується оптимальний процес або стан, тобто екстремальне значення показника якості, називаються оптимальними. Відшукання оптимальних параметрів системи – мета завдання оптимізації.

Завдання оптимізації розділяються на детерміновані і вірогідні – стохастичні.

Детерміновані завдання характеризуються тим, що критерій оптимальності є детермінованою функцією параметрів, що оптимізуються.

Імовірнісні завдання характеризуються наявністю випадкових процесів.

При виборі методу рішення необхідно враховувати відсутність або наявність обмежень на параметри, що оптимізуються, або стани. Завдання без обмежень простіші (добре відомі).

Завдання з обмеженнями відносяться до завдань математичного програмування.

При цьому складність завдання значною мірою визначається видом критерію оптимальності і обмежень. Якщо вони лінійні то завдання з області лінійного програмування (вирішується просто).

Якщо не лінійні – нелінійне програмування (вирішується складно).

По числу екстремумів завдання бувають одно - і багато екстремальні.

По числу параметрів завдання, що оптимізуються, розділяють на одновимірні і багатовимірні.

АВМ загального призначення придатні для вирішення завдань оптимізації динамічних систем, що описуються звичайними диференціальними рівняннями без обмежень. Такі завдання відносяться до класу варіаційних і краєвих завдань із звичайними похідними.

2. Краєві і варіаційні завдання

При вирішенні технічних проблем виникають завдання по оптимізації динамічних властивостей системи. Вони в багатьох випадках приводять до рішення диференціального рівняння

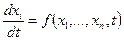
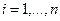
з краєвими умовами

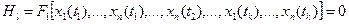
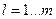
де 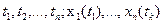- задані фіксовані значення незалежних змінних і відповідні значення незалежних змінних.

Завдання ідентифікації полягають у визначенні параметрів або виду правих частин рівнянь системи (1), щоб задовольнити умовам більш загального вигляду:

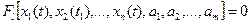
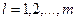
де, 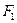- задані функціонали, що розповсюджуються на весь інтервал інтеграції; 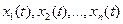- функції, що є рішенням початкової системи диференціальних рівнянь; 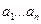- параметри, що підлягають визначенню для задоволення заданої умови.

Для завдань оптимізації параметри системи повинні бути вибрані так, щоб рішення її обертало в мінімум або максимум деяку умову 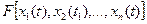, яка в цьому випадку називається критерієм оптимальності.

Майже всі існуючі методи вимагають багатократного рішення задачі Коші при різних значеннях початкових умов або параметрів системи. Процес рішення зводиться до пошуку необхідних значень, і методи рішення називаються пошуковими. До них відносяться:

1. Метод проб;

2. Метод комбінацій;

3. Метод близькостірішень;

4. Метод огляду;

5. Метод покоордінатной мінімізації;

6. Метод градієнта;

7. Метод найшвидшогоспуску.

Метод проб - застосовуеться для вирішення краєвих і варіаційних завдань. Спочатку виконується пробне рішення за довільних початкових умов. Для кожного варіанту оцінюється близькість отримуваного рішення до шуканому.

Метод комбінацій - використовується для вирішення завдань, що описуються лінійними диференціальними рівняннями. Зводиться до рішення n допоміжних завдань Коші з подальшим рішенням системи лінійних рівнянь алгебри щодо шуканих початкових умов.

Велика швидкодія АВМ в рішенні задачі Коші дозволяє швидко, використовуючи метод проб і, задаючись різними початковими умовами, досліджувати багато варіантів і вибрати що задовольняють граничним умовам або умовам оптимізації.

Метод огляду характеризується зміною параметрів за певною програмою, що не враховує результатів попередньої зміни змінних. Проводиться рівномірне сканування з постійним кроком в області допустимих значень параметрів. Недоліки:

- велика кількість пробних рішень

- великий час обчислень.

Застосовується рідко.

Метод покоордінатной мінімізації передбачає почерговузмінукожного елементу вектора Y при фіксованих значеннях решти елементів з переходом до зміни наступного параметра досягши приватного екстремуму залежності функціонала 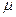вісі змінного параметра, коли, .

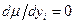Після циклу пошуку по всіх m параметрах знов починається зміна першого параметра, і цикл повторюється. Пошук продовжується поки всі частніпохідні 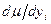не виявлятьсяблизькими до0.

Метод градієнта передбачає одночасну зміну всіх шуканих параметрів і характеризується необхідністю проведення пробних рішень для визначення напряму вектора градієнта.

Метод нашвидшого спуску - це варіант методу градієнта. Він відрізняється тим, що після визначення напряму вектора антиградієнта виконується не один, а декілька робочих кроків по вибраному напряму до тих пір, поки не буде досягнутий приватний мінімум функції 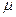по цьому напрямку. Новий напрям обирається аналогічно попередньому за допомогою m пробних кроків.

Розділ 5.