Методика рішення завдання розміщення
Уважаються заданими: площа регіону 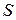 , кількість абонентів у мережі
, кількість абонентів у мережі  , капітальні витрати на установку одного ОЦ і АП
, капітальні витрати на установку одного ОЦ і АП  і
і 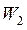 відповідно; вартість 1 км магістрального каналу зв'язку між ОЦ W3 і вартість 1 км каналу зв'язку між АП і ОЦ W4. Потрібно визначити координати установки ОЦ і АП, їхня кількість у регіоні, а також конфігурацію системи обміну даними, щоб забезпечити мінімум витрат і можливість обробки обсягів інформації.
відповідно; вартість 1 км магістрального каналу зв'язку між ОЦ W3 і вартість 1 км каналу зв'язку між АП і ОЦ W4. Потрібно визначити координати установки ОЦ і АП, їхня кількість у регіоні, а також конфігурацію системи обміну даними, щоб забезпечити мінімум витрат і можливість обробки обсягів інформації.
З очевидних геометричних міркувань треба, щоб капітальні витрати на магістральні канали зв'язку між ОЦ можна було б визначити з наступного вираження
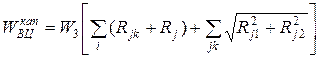 , (9)
, (9)
де 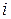 — індекс розглянутого ОЦ;
— індекс розглянутого ОЦ; 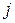 — індекси ОЦ, що перебуває праворуч й
— індекси ОЦ, що перебуває праворуч й 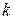 — який знаходиться нижче (див. рис. 2);
— який знаходиться нижче (див. рис. 2); 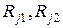 - проекція прямої, що зв'язує
- проекція прямої, що зв'язує 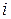 -й ОЦ із ОЦ, що перебувають нижче за діагоналлю, на вертикальну й горизонтальну осі координат, жорстко пов'язаних з контурами регіону.
-й ОЦ із ОЦ, що перебувають нижче за діагоналлю, на вертикальну й горизонтальну осі координат, жорстко пов'язаних з контурами регіону.
Величина  не залежить від значень
не залежить від значень 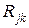 і
і 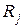 . У той же час відповідно до нерівності Коші друга сума у квадратних дужках формули (9) мінімізується при
. У той же час відповідно до нерівності Коші друга сума у квадратних дужках формули (9) мінімізується при 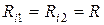 для будь-яких
для будь-яких 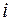 .
.
Ґрунтуючись на аналогічних міркуваннях, можна дійти висновку, що мінімізація сумарної довжини каналів зв'язку між ОЦ і АП також досягається при рівномірному розміщенні АП у зоні обслуговування ОЦ.
Виходячи з викладеного, визначають капітальні вкладення на створення усіх ОЦ 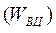 до АП
до АП 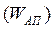 , що обслуговуються у регіоні. Опускаючи проміжні алгебраїчні перетворення у формулах, отриманих з геометричних побудов, наведемо основне співвідношення для постановки завдання мінімізації витрат на проектовану мережу:
, що обслуговуються у регіоні. Опускаючи проміжні алгебраїчні перетворення у формулах, отриманих з геометричних побудов, наведемо основне співвідношення для постановки завдання мінімізації витрат на проектовану мережу:
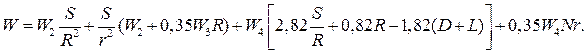 , (10)
, (10)
де  і
і 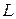 - розміри зони, заданої у вигляді прямокутника (див. рис. 2).
- розміри зони, заданої у вигляді прямокутника (див. рис. 2).
Для конкретних структур мережі ЕОМ значення 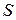 ,
,  ,
, 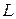 і
і  можуть бути обрані з деякої безлічі варіантів. Зокрема, з урахуванням рекомендацій про рівномірний розподіл ОЦ і АП у регіоні значення
можуть бути обрані з деякої безлічі варіантів. Зокрема, з урахуванням рекомендацій про рівномірний розподіл ОЦ і АП у регіоні значення 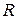 й
й 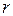 для будь-якого варіанта можуть бути обчислені у такий спосіб:
для будь-якого варіанта можуть бути обчислені у такий спосіб:
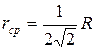 , (11)
, (11)
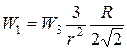 , (12)
, (12)
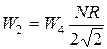 . (13)
. (13)
Знайдемо частки похідні від повних витрат W за змінним R та г з метою визначення екстремальних значень цих величин для функції W і дорівняємо їх до нуля:
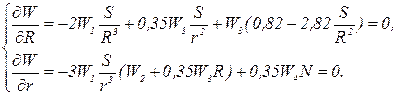 (14)
(14)
Розв’язавши спільно ці два рівняння як систему шляхом підстановки, одержимо шукане співвідношення, що є рівнянням 11-й ступеня відносно R:
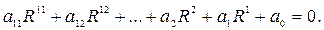 (15)
(15)
Вираження для коефіцієнтів 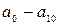 у загальному виді надзвичайно громіздкі, тому розглянемо приклад розрахунку з наступними даними:
у загальному виді надзвичайно громіздкі, тому розглянемо приклад розрахунку з наступними даними: 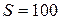 км2;
км2; 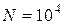 ;
; 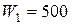 тис. грн.;
тис. грн.; 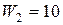 тис. грн.;
тис. грн.; 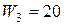 тис. грн. /км;
тис. грн. /км; 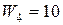 тис. грн. /км.
тис. грн. /км.
Знайшовши корінь алгебраїчного рівняння для даних значень коефіцієнтів, знайдемо безліч значень кореня 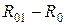 . Із цієї безлічі, природно, виключаються елементи, що визначають уявні й негативні значення, інші перевіряються на відповідність фізичному змісту завдання. Вибравши одне найбільш відповідне значення
. Із цієї безлічі, природно, виключаються елементи, що визначають уявні й негативні значення, інші перевіряються на відповідність фізичному змісту завдання. Вибравши одне найбільш відповідне значення 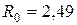 км, знаходимо далі відповідному цьому значенню величини, що визначають оптимальний розподіл витрат для синтезованої мережі:
км, знаходимо далі відповідному цьому значенню величини, що визначають оптимальний розподіл витрат для синтезованої мережі:
1) середня відстань між АП і ОЦ: 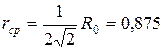 км;
км;
2) оптимальне число вузлів (ОЦ у цьому випадку) у мережі:
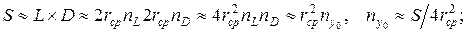
3) середнє число АП, що приєднують у кожному вузлі,
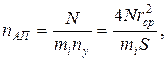
де  — середнє число абонентів в одному вузлі.
— середнє число абонентів в одному вузлі.
Для топологічного проектування з перерахованих параметрів найбільш важливим є оптимальна кількість вузлів у мережі. У тих випадках, коли вартість є головним критерієм, синтез топологічної структури може бути проведений за мінімумом цього критерію.
Допустимо, що для деяких значень вихідних даних 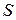 ,
,  ,
, 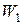 ,
, 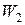 ,
, 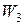 ,
, 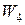 був отриманий результат, який відповідає оптимальному числу
був отриманий результат, який відповідає оптимальному числу 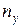 . Реальне розміщення ОЦ по території регіону може не відповідати рівномірному їхньому розподілу. Але при невеликій кількості вузлів шляхом підбору конкретних місць розташування ОЦ, можна вибрати найбільш близький реальний варіант і прийняти його для наступного аналізу.
. Реальне розміщення ОЦ по території регіону може не відповідати рівномірному їхньому розподілу. Але при невеликій кількості вузлів шляхом підбору конкретних місць розташування ОЦ, можна вибрати найбільш близький реальний варіант і прийняти його для наступного аналізу.
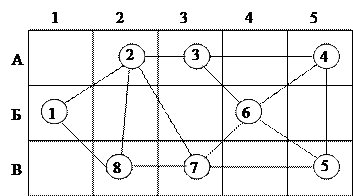
Припустимо, що у результаті обчислень 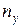 вийшло дорівненим восьми, а реальне місце розташування ОЦ, поєднуваних у мережу, відповідає схемі, показаної на рис. 3.
вийшло дорівненим восьми, а реальне місце розташування ОЦ, поєднуваних у мережу, відповідає схемі, показаної на рис. 3.
При первісних припущеннях, уважалося, що зв'язки між вузлами утворять повнозв’язну структуру. Однак під час синтезу архітектури такої мережі можна теоретично розглянути й інші варіанти топологічних структур, оцінити, наскільки можливо подальше зменшення вартості, якщо це потрібно.
 Надалі при розгляді питання синтезу топології ІМ будемо орієнтуватися на просту структуру типу дерева, думаючи, що у такий спосіб можна понизити вартість проектованої мережі й зрівняти її з максимальною у відповідності до повнозв’язної структури.
Надалі при розгляді питання синтезу топології ІМ будемо орієнтуватися на просту структуру типу дерева, думаючи, що у такий спосіб можна понизити вартість проектованої мережі й зрівняти її з максимальною у відповідності до повнозв’язної структури.
Рисунок 3 - План розміщення вузлів у синтезованій мережі
Для рішення завдання мінімізації структури скористаємося моделлю мережі у вигляді зваженого графа, у якого ваги дуг характеризують, наприклад, довжини каналів між відповідними вузлами ІМ. Тому що розглядається мережа з відносно малою кількістю ребер, для неї зручним способом рішення завдання мінімізації структури є алгоритм Краскала, що полягає в наступному [12].
Таблиця 1 – Список ребер з їхніми ваговими значеннями
| Вага ребра | Ребра | Примітка |
| 0,5 | (1,2) | – |
| 1,0 | (1,8), (3,6), (6,7) | – |
| 1,8 | (3,7) відкидаємо | Приводить до циклу |
| 1,9 | (2,3), (2,7) відкидаємо | – |
| 2,0 | (2,6) відкидаємо | – |
| 2,1 | (7,8) відкидаємо | – |
| 2,2 | (1,7) відкидаємо | – |
| 2,3 | (1,3), (4,5) і (1,3) | (1,3) відкидаємо |
| 2,8 | (1,6) відкидаємо | – |
| 3,0 | (6,4) | – |
| 3,5 | (3,4) відкидаємо | – |
| 5,5 | (5,6) відкидаємо | – |
| 5,8 | (5,7) відкидаємо | – |
| 8,0 | (1,5) відкидаємо | – |
Упорядкуємо ребра за вагою, вибираючи з безлічі ребер графа, при складанні списку, щораз ребро мінімальної ваги, і далі за зростанням, як показано в табл. 1.
Потім, користуючись списком, будуємо мінімальне покриваюче дерево, починаючи з першого ребра й додаючи наступні один по одному. Якщо чергове обране ребро приводить до утворення циклу, то його відкидаємо. Після вибору ребра 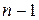 (
( 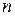 -число вершин графа) процес закінчується.
-число вершин графа) процес закінчується.
Дата добавления: 2021-12-14; просмотров: 508;











