Решить аналогичную задачу, если прямые заданы общими уравнениями в аффинных координатах.

Решение

Перейдем от общих уравнений прямых в аффинных координатах к общим уравнениям этих прямых в однородных координатах (см. задачу 3 из практического занятия 5). После этого воспользуемся решением предыдущей задачи.

Обратить внимание на двойственность понятий двойное отношение четырех точек на проективной прямой и двойное отношение четырех прямых пучка на проективной плоскости.

Тема 4. Линии 1 порядка на проективной плоскости.Второе занятие.

Список необходимых сведений.Гармонические четверки точек и прямых. Теорема Дезарга.

Практические задания

Решение задач, аналогичных рассмотренным в практическом занятии №6, в случае гармонического отношения четырех точек проективной прямой или четырех прямых пучка.

Решение

Напомним, что точки прямой (прямые пучка) находятся в гармоническом отношении, если 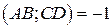. Далее решения задач из практического занятия 6 повторяются дословно.

Построение четвертой гармонической точки прямой или четвертой гармонической прямой пучка для трех данных точек или прямых соответственно.

Решение см., например, в [4 , с. 44].

Сделать рисунки к теореме Дезарга в случаях, когда

А) центр и ось перспективы являются бесконечно удаленными элементами пополненной плоскости,

Б) центр перспективы является бесконечно удаленной точкой пополненной плоскости, а ось перспективы – обыкновенной прямой этой плоскости,

В) ось перспективы является бесконечно удаленной прямой пополненной плоскости, а центр перспективы – обыкновенной точкой этой плоскости.

Сформулировать соответствующие теоремы аффинной геометрии.

Решение задач на аффинной плоскости с использованием теоремы Дезарга.

Множество таких задач содержится в углубленном курсе элементарной геометрии. См., например, [19].

Обратить внимание на двойственность прямой и обратной теорем Дезарга. Обсудить понятие двойственных фигур, привести примеры двойственных фигур.