Практические задания
1. На проективной плоскости даны две точки 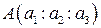 и
и 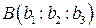 своими координатами относительно некоторой проективной системы координат R. Написать параметрическое и общее уравнения прямой, проходящей через точки А и В.
своими координатами относительно некоторой проективной системы координат R. Написать параметрическое и общее уравнения прямой, проходящей через точки А и В.
Решение.
1) Параметрическое уравнение прямой имеет вид
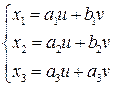 ,
,
где u, v произвольные действительные числа.
2) Общее уравнение прямой найдем из уравнения

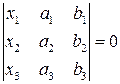 .
.
Найти координаты точки пересечения прямых, если заданы по две точки на каждой из них.
Решение.
1) Напишем общие уравнения прямых, проходящих через заданные точки. Для этого используем решение предыдущей задачи.
2) Решим систему из двух уравнений, найденных в пункте 1), и найдем координаты 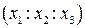 их точки пересечения.
их точки пересечения.
Найти двойное отношение четырех точек на проективной прямой
A 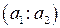 , B
, B 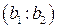 , C
, C 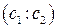 , D
, D 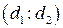 .
.
Решение.
По определению двойного отношения
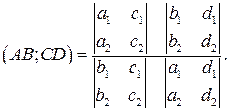
На проективной прямой дано двойное отношение четырех точек и координаты трех из них. Найти координаты четвертой точки, если
(AB,CD)=k, A 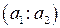 , B
, B 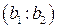 , C
, C 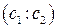 .
.
Решение.
Обозначим координаты точки D через 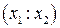 . По условию и по определению двойного отношения
. По условию и по определению двойного отношения
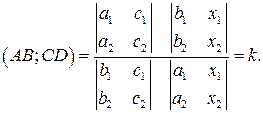
Получим
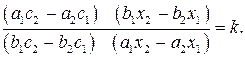
Координаты 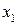 и
и 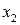 не могут одновременно равняться нулю.
не могут одновременно равняться нулю.
Если, например, 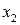
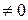 , то можно разделить числитель и знаменатель дроби на
, то можно разделить числитель и знаменатель дроби на 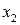 . Получим
. Получим
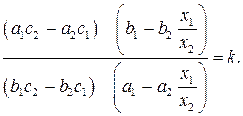
Решив это уравнение относительно 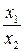 , получим численное значение
, получим численное значение 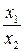 =
= 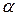 .
.
Тогда координаты точки D будут 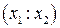 =
= 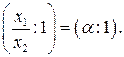
Замечание. Если 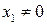 , то можно делить на
, то можно делить на 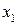 и решать аналогично.
и решать аналогично.
5. На проективной плоскости дано двойное отношение четырех точек и координаты трех из них. Найти координаты четвертой точки, если (AB,CD)= -1, A 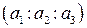 , B
, B 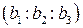 , C
, C 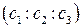 . Проверитьколлинеарность точек A, B, C.
. Проверитьколлинеарность точек A, B, C.
Решение
1) Проверим коллинеарность точек А, В, С.
Точки A 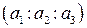 , B
, B 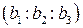 , C
, C 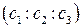 порождаются векторами a
порождаются векторами a 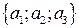 , b
, b 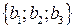 , c
, c 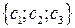 . Точки лежат на одной прямой тогда и только тогда, когда векторы a, b, c линейно зависимы. Чтобы установить это или опровергнуть, проверим равенство или соответственно неравенство нулю определителя
. Точки лежат на одной прямой тогда и только тогда, когда векторы a, b, c линейно зависимы. Чтобы установить это или опровергнуть, проверим равенство или соответственно неравенство нулю определителя
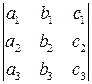 .
.
Если определитель равен нулю, то точки коллинеарны. В противном случае неколлинеарны.
2) При условии что точки коллинеарны, найдем координаты четвертой точки D.
Замечание. Эту задачу нельзя решать как предыдущую, так как нам известны не две, а три координаты точек. Для формул же двойного отношения точки должны иметь по две координаты.
Теорема. Пусть на проективной плоскости задана проективная система координат R={E1,E2,E3,E} и точка М имеет координаты 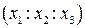 относительно R.
относительно R.
Пусть 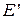 и
и 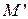 - проекции точек Е и М из центра
- проекции точек Е и М из центра 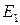 на прямую
на прямую 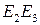 ,
,
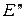 и
и 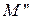 - проекции точек Е и М из центра
- проекции точек Е и М из центра 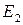 на прямую
на прямую 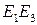 ,
,
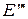 и
и 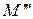 - проекции точек Е и М из центра
- проекции точек Е и М из центра 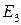 на прямую
на прямую 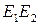 .
.
Тогда точки 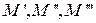 имеют координаты
имеют координаты
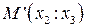 на прямой
на прямой 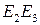 относительно R={E2,E3,E
относительно R={E2,E3,E 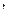 },
},
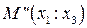 на прямой
на прямой 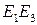 относительно R
относительно R 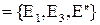 ,
,
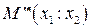 на прямой
на прямой 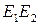 относительно R
относительно R 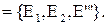
Теорема. При центральном проектировании двойное отношение точек не меняется, то есть двойное отношение точек равно двойному отношению их образов.
Рассмотрим проекции 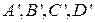 точек A, B, C, D на прямую
точек A, B, C, D на прямую 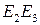 .
.
В силу теорем
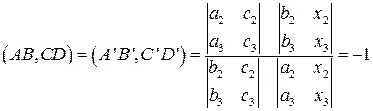 , (1)
, (1)
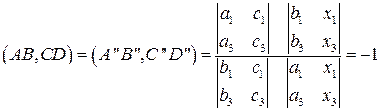 , (2)
, (2)
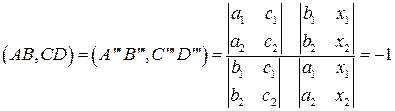 . (3)
. (3)
Координаты 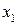 ,
, 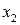 ,
, 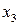 не могут одновременно равняться нулю.
не могут одновременно равняться нулю.
Если, например, 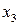
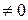 , то в равенствах (1) и (2) можно разделить числитель и знаменатель дроби на
, то в равенствах (1) и (2) можно разделить числитель и знаменатель дроби на 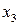 . Равенство (3) в этом случае нам не понадобится. Из (1) и (2) найдем численные значения
. Равенство (3) в этом случае нам не понадобится. Из (1) и (2) найдем численные значения 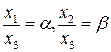 .
.
Получим для координат точки 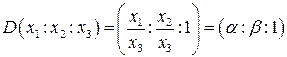 .
.
Если 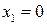 , то либо
, то либо 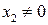 , либо
, либо 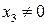 . Выберем ту координату
. Выберем ту координату 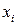 , для которой
, для которой 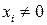 и повторим для нее рассуждения как для координаты
и повторим для нее рассуждения как для координаты 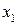 .
.
6. На проективной плоскости прямые a, b, c заданы уравнениями
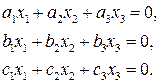
соответственно. Написать уравнение прямой d, если (a b , c d) = -1/3. Проверить принадлежность прямых a, b, c одному пучку.
Решение.
Выпишем координаты прямых
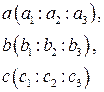
и повторим решение задачи 5, поменяв слова «точка» и «прямая» местами. Мы воспользовались принципом двойственности точек и прямых на проективной плоскости.
Дата добавления: 2021-12-14; просмотров: 560;











