Определение динамических реакций в точках закрепления оси вращающегося твердого тела

Рассмотрим тело, вращающееся с угловой скоростью 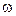и угловым ускорением 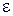вокруг неподвижной оси, закрепленной в подшипниках А и В

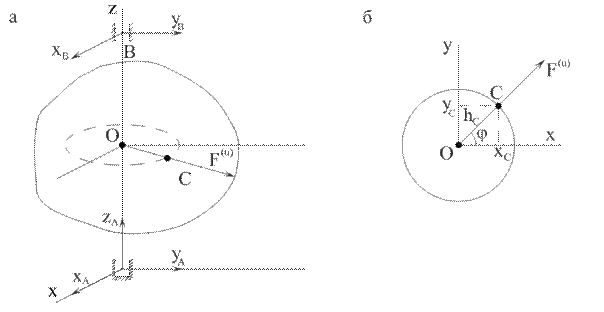Рис. 6.6

(рис. 6.6, а). Найдем динамические реакции 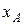, , 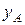, , 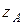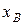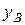подшипников, действующие на ось, т.е. реакции, возникающие при вращении тела. Пусть на тело действуют заданные внешние силы 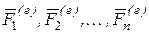, главный вектор которых обозначим через 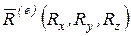, координатные оси Охуz показаны на рисунке. Главный момент внешних сил обозначим через 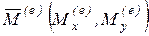. Для определения искомых реакций воспользуемся принципом Д’Аламбера (6.9). Обозначим 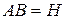, тогда эти уравнения примут вид

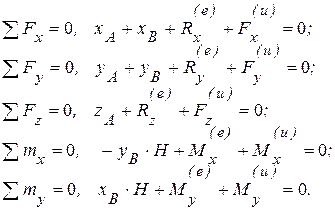(6.15)

Главный вектор сил инерции 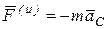и приложен в точке С –центре масс. При движении тела, центр масс С имеет нормальную 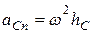и касательную 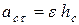составляющие ускорения, где 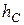- расстояние точки С от оси вращения. Следовательно, вектор 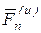совпадает с направлением ОС, вектор 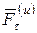направлен перпендикулярно вектору 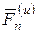(рис. 6.7,б).

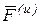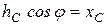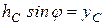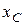Вычисляя проекции на оси координат и учитывая, что , , где и 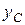- координаты центра масс, имеем:

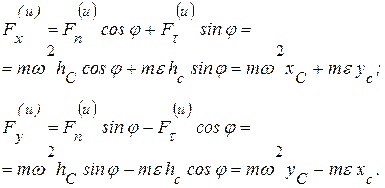(6.16)

Вычислим моменты от сил инерции. Для этого рассмотрим частицу массой 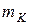определяемую радиус-вектором 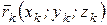, отстоящую от оси вращения на 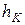(рис.6.7,а). Для нее сила инерции имеет нормальную 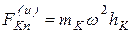и касательную 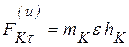составляющие. Тогда, аналогично (6.16), имеем:

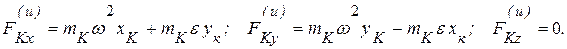
Тогда:

.

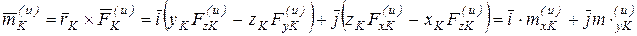Вычислим

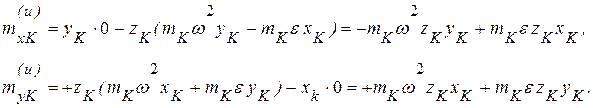
Суммируя эти выражения по всем точкам системы, получим

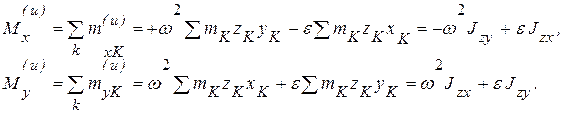(6.17)

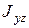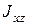Здесь и - центробежные моменты инерции. Подставляя (6.16) и (6.17) в (6.15), получим

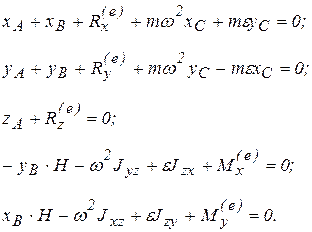(6.18)

Уравнения (6.18) определяют динамические реакции, действующие на ось вращения Оz.

Назовем условно статическими реакциями те значения реакций, которые дают уравнения (6.18), если предположить 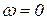и 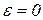. Из уравнений (6.18) видно, что динамические реакции могут быть значительно больше статических, причем это зависит не только от значения 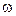и 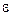, но и от величин 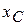, , 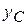, , 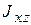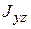характеризующих распределение масс тела по отношению к оси вращения Оz.

Из уравнений (6.18) видно, что для того, чтобы динамические реакции были равны статическим, при w 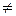0, e 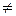0, должны выполняться следующие условия

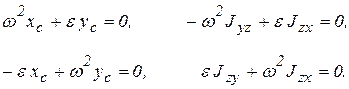(6.19)

Так как определитель этих двух систем однородных уравнений равен 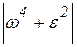и всегда не равен нулю, то этим уравнениям удовлетворяют только следующие значения переменных

x_c=0, y_c=0, J_xz=0, J_yz=0.

Эти равенства показывают, что ось вращения z должна

1. проходить через центр масс С тела;

2. совпадать с одной из главных осей инерции тела.

В этом случае говорят, что вращающееся тело динамически уравновешено на оси вращения, а ось вращения называют свободной осью.

Задача динамического уравновешивания вращающихся тел играет очень большую роль в машиностроении, так как угловые скорости современных машин достигают весьма больших значений.

Предположим, что тело динамически не уравновешено, тогда возможны два частных случая:

1. Центр масс С лежит на оси вращения, но ось вращения не является главной.

2. Центр масс С не лежит на оси вращения.

Практически очень важно уметь любую ось вращения сделать главной центральной осью инерции. Для этого прибавляют к телу две (одну) точечные массы. Покажем, как это делается. Пусть тело массы М вращается вокруг оси z. Ось вращения не проходит через центр масс, прибавим к телу две массы 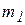и 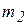в точках с координатам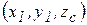и и .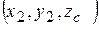

Тогда, чтобы оси стали главными центральными осями, необходимо, чтобы центр масс и центробежные моменты инерции полученной системы были равны нулю. Согласно формулам (2.2) и (2.12) из лекции 2, следует, что если

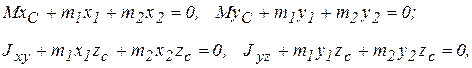(6.20)

то для полученного тела будет 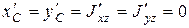, т.е. ось Оz станет главной центральной осью инерции. Вычислить координаты x₁, x₂, y₁, y₂ из системы четырех линейных уравнений (6.20) не сложно. Такой метод уравновешивания масс широко используется в технике. Обычно окончательная балансировка проводится на специальных стендах.

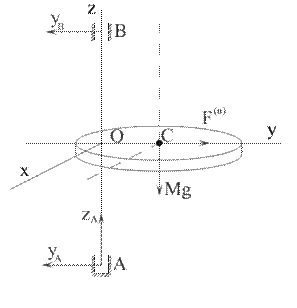Рис. 6.7

Для определения давлений на ось в отдельных конкретных задачах обычно не пользуются готовыми уравнениями (6.18), а каждый раз применяют принцип Д’Аламбера.

Пример 4. Ось вращения диска радиусом R перпендикулярна к его плоскости (рис. 6.7) и смещена от центра масс на расстояние а. Вес диска равен Mg, угловая скорость постоянна и равна 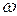. Определить динамические реакции подшипников А и В, если 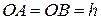. Провести динамическую балансировку.

Решение. Проведем вращающиеся вместе с телом оси Охуz так, чтобы ось Оу прошла через центр масс С диска (рис. 6.7). Ось Оz будет главной осью инерции по отношению к точке О, поскольку плоскость Оху является плоскостью симметрии диска. Тогда

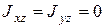(см. лекция 2, формула 2.14), и из условия 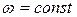и формул (6.17) вытекает, что 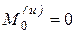. Следовательно, силы инерции приводятся к одной равнодействующей F^(u), проходящей через точку О, и направлены вдоль линии ОС (вдоль оси Оу). По модулю 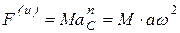. Так как силы Мg и 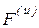лежат в плоскости Оуz, то реакции подшипников лежат в этой же плоскости, т.е. имеют составляющие 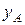, 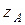в точке А и 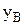в точке В.

Составим уравнения равновесия (6.15):

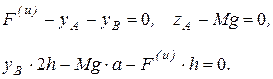
Решая эти уравнения, найдем:

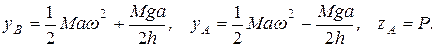
Реакци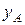и и 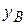все время располагаются в плоскости Оуz, вращающейся вместе с телом.

Для динамического уравновешивания масс добавим тело весом mg на расстояние 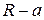от начала координат влево вдоль оси у (рис. 6.8). Тогда возникнет еще одна сила инерции 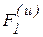, проходящая через точку О и направленная против оси Оу. По модулю 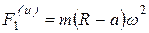. Симметрия задачи не нарушена. Составим уравнения равновесия (6.15):

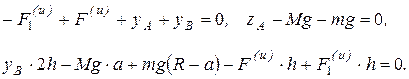(а)

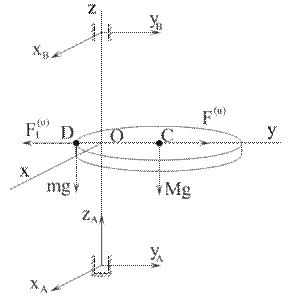Рис. 6.8

Вычислим величину добавленной массы m с помощью (6.20):

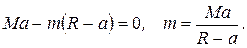
Подставим полученное значение m в (а) и вычислим реакции опор:

.

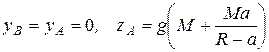Добавив массу m, можно добиться нулевого давления на ось, что мы и сделали.