Вращающегося вокруг неподвижной оси
Вычислим координаты главного момента сил инерции твердого тела (6.12), вращающегося вокруг неподвижной оси. Ось Оz совместим с осью вращения, а оси Ох и Оу скрепим с вращающимся телом (рис.6.3а), тогда 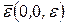 и
и  ,
, 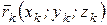 - радиус – вектор рассматриваемой точки
- радиус – вектор рассматриваемой точки 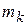 . При вращении тела вокруг неподвижной оси Оz ускорение любой точки
. При вращении тела вокруг неподвижной оси Оz ускорение любой точки 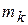 состоит из нормального ускорения
состоит из нормального ускорения 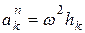 и касательного ускорения
и касательного ускорения 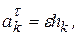 где
где 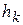 - расстояние точки k от оси вращения Оz (рис.6.3,б):
- расстояние точки k от оси вращения Оz (рис.6.3,б):
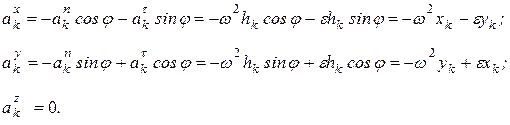
 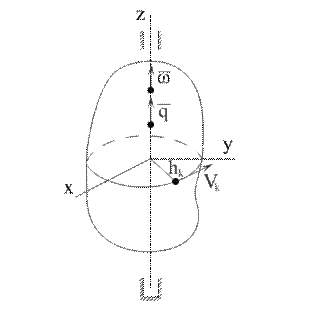 Рис. 6.3 Рис. 6.3
|
Здесь учтено, что 
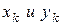 - координаты точки
- координаты точки 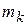 .
.
Тогда, согласно (6.12), получим,
|
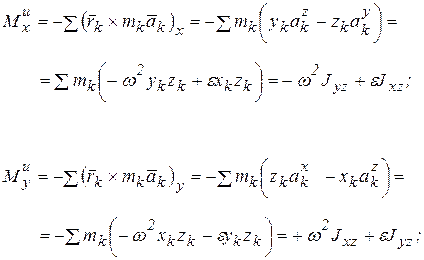
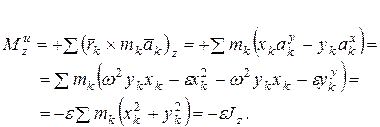
Здесь 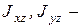 центробежные моменты инерции,
центробежные моменты инерции, 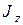 осевой момент инерции.
осевой момент инерции.
Таким образом, главный момент сил инерции твердого тела, вращающегося вокруг неподвижной оси, сводится к паре сил, момент которой равен
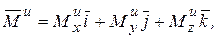 (6.14)
(6.14)
где
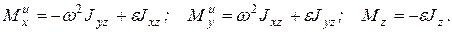
Если ось вращения проходит через центр тяжести тела и оси xyz являются главными осями, то
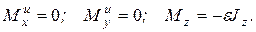 (6.14а)
(6.14а)
Пример 3. Через блок весом 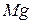 и радиусом R перекинута нерастяжимая нить, на конце которой подвешен груз А весом
и радиусом R перекинута нерастяжимая нить, на конце которой подвешен груз А весом 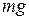 . Определить ускорение а груза А, натяжение нити Т и давление на подшипник оси блока (рис. 6.4).
. Определить ускорение а груза А, натяжение нити Т и давление на подшипник оси блока (рис. 6.4).
Решение. Пусть груз А опускается вниз, тогда сила инерции груза вверх. 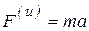 .
.
Поскольку ось вращения диска является осью симметрии, то
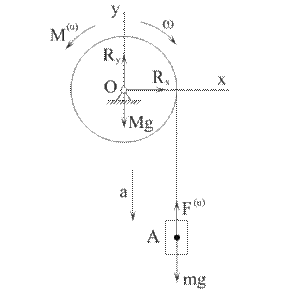 Рис. 6.4
Рис. 6.4
|
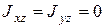 .Следовательно, момент от сил инерции, согласно (6.14), равен
.Следовательно, момент от сил инерции, согласно (6.14), равен 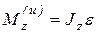 и направлен в сторону противоположную вращению диска.
и направлен в сторону противоположную вращению диска.
Отбросим опору О, заменим ее действие реакциями подшипника 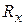 и
и 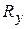 (рис 6.4). Составим уравнения кинетостатики (6.9):
(рис 6.4). Составим уравнения кинетостатики (6.9):
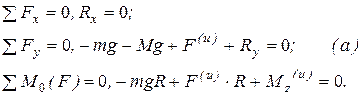
 Рис. 6.5
Рис. 6.5
|
Подставим в последнее уравнение значения силы инерции 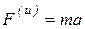 и момента от сил инерции
и момента от сил инерции 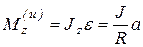
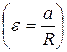 и решим его относительно ускорения а, получим
и решим его относительно ускорения а, получим
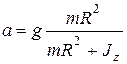 .
.
Тогда из первых двух уравнений определим
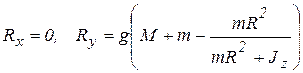 .
.
Для определения натяжения нити разорвем гибкую связь и заменим ее действие натяжением Т (рис. 6.5). Добавляя внешнюю силу 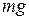 и силу инерции
и силу инерции 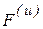 , имеем
, имеем
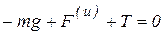 ,
,
откуда 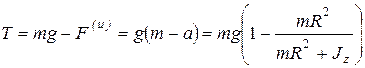 .
.
Если считать диск сплошным телом, то 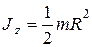 , тогда
, тогда
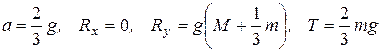 .
.
Дата добавления: 2019-12-09; просмотров: 845;











