Принцип Д’Аламбера для материальной точки
Уравнение движения материальной точки массой m относительно инерциальной системы отсчета под действием приложенных сил, равнодействующая которых 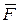 , имеет вид
, имеет вид
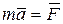 . (6.1)
. (6.1)
Перепишем это уравнение в виде
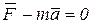 . (6.2)
. (6.2)
Введя обозначение
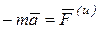 , (6.3)
, (6.3)
получим
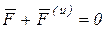 . (6.4)
. (6.4)
Вектор 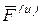 , равный по модулю произведению массы точки на ее ускорение и направленный противоположно вектору ее ускорения, называется силой инерции.
, равный по модулю произведению массы точки на ее ускорение и направленный противоположно вектору ее ускорения, называется силой инерции.
Уравнение (6.4) выражает принцип (уравнение) Д’Аламбера: в каждый момент движения геометрическая сумма внешних сил и силы инерции равна нулю.
При этом следует иметь в виду, что к материальной точке приложена только равнодействующая сила 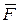 т.е. внешняя сила и реакция связи, если точка не свободна. Сила же инерции к точке не приложена, а появляется при движении точки.
т.е. внешняя сила и реакция связи, если точка не свободна. Сила же инерции к точке не приложена, а появляется при движении точки.
Метод кинетостатики является формальным приемом сведения уравнения динамики к уравнению статики, причем при решении практических задач
такой прием обладает рядом достоинств.
Пример 1. Шарик массой m подвешен на нити длиной L. Шарику сообщают равномерное движение по окружности в горизонтальной плоскости (рис. 6.1). Нить составляет угол 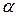 с вертикалью. Определить скорость шарика и натяжение нити.
с вертикалью. Определить скорость шарика и натяжение нити.
Решение. Направим ось Оу вертикально вниз, а плоскость хОу пусть проходит через шарик в рассматриваемый момент времени (рис. 6.1).При равномерном движении по окружности точка имеет ускорение
 ,
,
 Рис. 6.1
Рис. 6.1
|
направленное по оси Оx к центру окружности, т.е. к точке О. Сила инерции направлена по оси Оx против направления 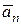 и по модулю (согласно 6.3), равна
и по модулю (согласно 6.3), равна
 .
.
Далее освободимся от связи, заменим ее силой натяжения Т. Составим уравнение Д’Аламбера (6.4) (уравнение кинетостатики):
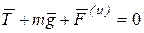 .
.
Перейдем от векторного уравнения к скалярному. Для чего спроецируем полученное уравнение на координатные оси
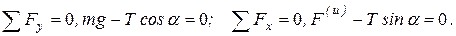
Отсюда находим
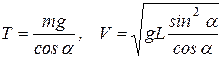 .
.
Дата добавления: 2019-12-09; просмотров: 682;











