Принцип Д’Аламбера для механической системы

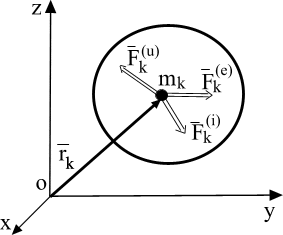Рис. 6.2

Рассмотрим материальную точку массой 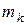системы, состоящей из N точек (рис. 6.2). Обозначим ускорение этой точки 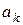, равнодействующую внешних сил через 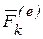, равнодействующую внутренних сил, приложенных к той же точке через 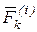. Реакции связей входят в 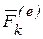. Тогда принцип (6.4) будет иметь вид

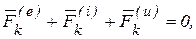(6.5)

где .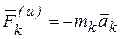

Складывая почленно все N уравнений (6.5), получим

(6.6)

Первая сумма в уравнении (6.6) равна главному вектору 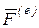внешних сил, приложенных к системе; вторая сумма равна нулю, поскольку геометрическая сумма всех внутренних сил системы равна нулю (3.1); последняя – главному вектору 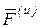сил инерции. Таким образом, (6.6) запишем как

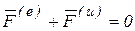, (6.7)

т.е. в каждый момент времени сумма главных векторов внешних сил и сил инерции движущейся системы равна нулю.

Выберем произвольный полюс О и проведем из него к точке 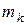радиус-вектор 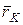(рис. 6.2). Умножая каждое слагаемое из (6.6) векторно на соответствующий радиус-вектор слева и складывая все N полученных таким образом уравнений, имеем

.

Первая сумма равна главному моменту 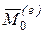внешних сил, приложенных к системе; вторая сумма равна нулю (3.2), а последняя – главному моменту сил инерции. Следовательно,

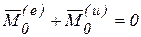, (6.8)

т.е. в каждый момент времени сумма главных моментов внешних сил и сил инерции движущейся механической системы равна нулю.

Двум векторным уравнениям (6.7) и (6.8) соответствуют шесть уравнений в проекциях на оси декартовых координат

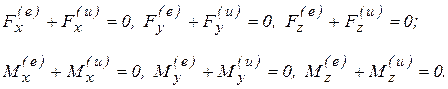(6.9)

Движение твердого тела, как частный случай механической системы, вполне определяется этими шестью уравнениями. Если рассматривается система, состоящая из нескольких тел, то можно составить соответствующие уравнения для каждого тела в отдельности.