ИНДИВИДУАЛЬНЫЙ ПРОГНОЗ

Для того чтобы прогнозировать сроки службы изделий, необходимо разработать методы определения их будущего состояния по данным, полученным в прошлом и настоящем. В принципе эта задача неопределенная, поскольку все про­цессы в машинах имеют элементы случайности, поэтому прогноз может быть выполнен с определенным риском. Однако достаточно убедительная предыстория позволяет с определенной уверенностью прогнозировать будущее состояние изделия.

Рассмотрим два способа обработки исходной информации. При всех способах прогнозирования предполагается, что проведены предварительные исследования (исходная информация) в. широком диапазоне изменения диагностических сигналов, соответствующих изменению технического состояния изделия.

а б.

Рис. 6. Реализация изменения диагностических сигналов

Предположим сперва, что этот материал можно представить некоторыми реализациями (графиками) вида показанного на рис. 6а и 6б в функции времени работы изделия t. Поскольку измерения проводятся в некоторые дискретные моменты времени реализации имеют вид ломанных, которые можно аппроксимировать плавными кривыми. Аппроксимация плавными кривыми выполняется обычно методом наименьших квадратов. -

Задают вид аппроксимирующего выражения. Обычно в форме

U = a t^b (1)

где а и b неизвестные параметры.

Логарифмируя это выражение, преобразуют его к более простому виду

Ln U = ln a+b ln t

. Обозначают

ln U=y ,ln a= a₀ ,ln t= x

Теперь

y= a₀+ b x.

Неизвестны параметры а₀ и Ь. Для их определения составляют выражение суммарной квадратичной ошибки аппроксимации

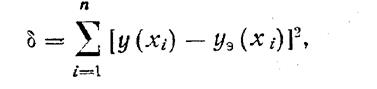
где y_э(x_i)—экспериментальное значение параметра y.

Его получают пересчетом значений U, соответствующих по формулам. После чего имеют график y_э (x) (рис. 7 ) у(х_i)— предполагаемое значение параметра.

Рис. 7. К аппроксимации экспериментальных данных.

Подставляя, получим

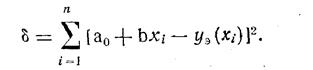
Неизвестные параметры а₀ и b определяются из условия минимума ошибки аппроксимации δ. Условия минимума имеют вид

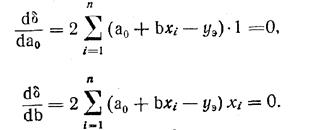
Откуда, окончательно, имеем

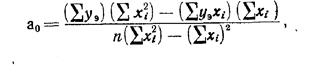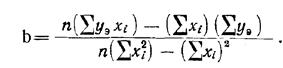.(2) .(3)

Теперь осталось определить по а₀ исходный параметр а. Очевидно, что,

a = e

Расчеты показывают, что обычно для одного и того же процесса изменение параметра b незначительно от изделия к изделию. Как правило, в широких пределах изменяется параметр а. Ориентировочные данные по параметру b определяются из таблиц.

На этом принципе основан метод прогнозирования технического состояния по одному измерению, который заключается в следующем. Пусть известна наработка изделия и значение параметра U₁ в этот момент. Тогда задаваясь видом изменения параметра в форме (1), получим

U₁= a t₁^b ,

где b задано

Отсюда

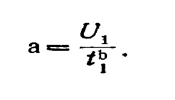
Задаваясь предельным значением параметра U = U_n имеем

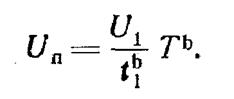
где Т — наработка до предельного состояния. Отсюда

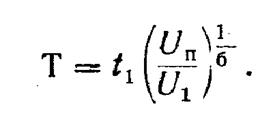
При таком подходе предполагается, что дальнейшее, после момента t₁, изменение параметра U происходит по зависи­мости (1) с уже постоянным параметром а присущим дан­ному конкретному изделию (рис. 8).

Если до предельного состояния имеется возможность по­лучить еще ряд значений па­раметра U_i при наработках t_i, то •производят корректировку параметров а и b по формулам приведенным выше (2,3).

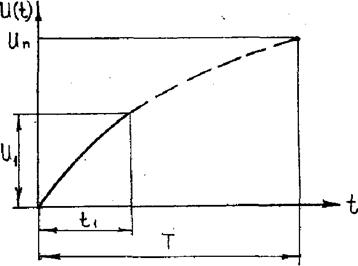
Рис.8. Индивидуальный прогноз долговечности изделий.

Изложенный выше способ прогнозирования получил название прогнозирования по реализации.

Определение вида функциональной зависимости U=f(t) изложенным выше методом по реализациям изменения параметров, представляет определенные трудности, так как требует проведения большого объема экспериментальных исследований. ,

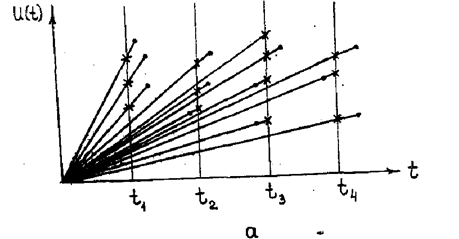
Рис. 9, Статистическое прогнозирование долговечности.

Для сокращения объема работ и при отсутствии реализа­ции может быть применен способ, получивший название статистического и заключающийся в следующем. Измеряют диагностические параметры большого числа однотипных изделий при различных наработках. Результаты измерений можно изобразить графически в виде поля точек.

Затем проводят сечения при наработках t₁, t₂,, t₃,, t₄.. Интервалы t₂—t₁, t₃—t_2, т. д. одинаковы. Путем линейной интерполяции и экстраполяции все точки лежащие рядом с проведанными сечениями сносят на них (рис. 9).

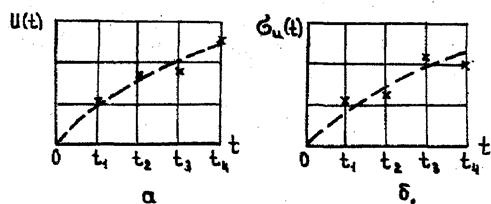
Рис. 10. Математическое ожидание и среднеквадратическое отклонение параметра.

В каждом сечении t== t_i строят распределение параметра и рассчитывают его математическое ожидание U(t) и сред­неквадратичное отклонение σ_u(t)(рис.10).

Полученные экспериментальные точки могут быть аппроксимированы аналитическими выражениями вида (1) с по­мощью формул (2) и (3).

Получим

Ū (t) = a₁ t^b1 ;σ_U (t) = a₂ t ^b2

Если ввести возможное отклонение параметра U от его среднего значения в долях σ_u(t) с помощью некоторого не­определенного коэффициента К, то возможную реализацию изменения параметра U(t} во времени можно представить в такой записи

U(t) = Ū (t) ± К σ_U (t) = a₁t^b1. + Кa₂t^b2

Придавая коэффициенту К ряд значений от нуля до ±3 через любые интервалы, можно построить серию возможных реализаций (рис. 11).

Теперь прогнозирование сводится к тому, что для наработки t=t₁ и параметра U(t₁) определяется реализация, соответствующая данному конкретному изделию, которая и используется в качестве прогнозирующей.

При этом предполагается, что процесс будет развиваться в дальнейшем в соответствии с этой реализацией. Возможна и корректировка прогноза. Если при t=t₂ параметр U₂ не попал на исходную реализацию, по видимому, целесообразно проинтерполировать между реализациями и уточнить ожидаемый срок службы (Т₁’ вместо T₁).

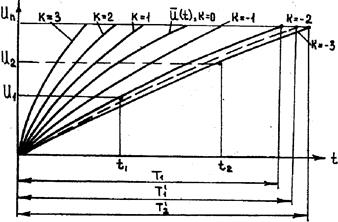
Рис. 11. Возможные реализации изменения пара­метра.

При диагностировании обычно пользуются понятием остаточного ресурса. Остаточный ресурс равен

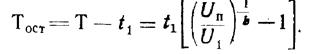
Это выражение определяет оставшийся после, момента диагностирования ресурс изделия до предельного состояния.

Определенный остаточный ресурс нельзя рассматривать как абсолютно точный. Дело в том, что по разным причинам (нестабильность условий испытаний, изменение поверхност­ных свойств материалов и т. д.) остаточный ресурс колеблется в некоторых пределах. Выражение (Т_ост) следует рассматривать как среднее значение остаточного ресурса. Тогда возможные его отклонения можно определить по формуле, полагая распределение остаточного ресурса нормальным

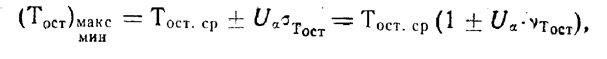
где ν_Тост —коэффициент вариации Тост (ошибка прогноза);

—квантиль нормального распределения.

Обычно интересуются минимальным гарантированным остаточным ресурсом

Тост. rap = Тост. ср (1—Uα ν_Тост).

Пример. В результате диагноза в момент t₁ = 210 сут, уста­новлено, что среднее увеличение шага в результате износа составляет U₁ = 0,635 Uп мм. Предельное увеличение шага принимается равным Uп. =6 мм; α==0,9, ν =0,25. Показатель b, как показали предшествующие исследования увеличения шага цепи транспортера во времени, равен единице (b = 1). Определить остаточный гарантированный ресурс транспортера

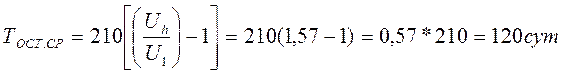
Теперь

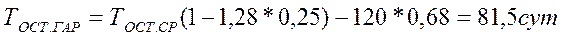
Таким образом, транспортер, подвергнутый диагностированию при t₁=210сут гарантированно проработает

Тгар. = 210+81,5~292 сут.

Если стать на позицию частичного ремонта, то его следует не ремонтировать в мастерской, а оставить для ремонта в условиях эксплуатации (Trap >60 сут, см предыдущий пример).

Индивидуальное прогнозирование можно использовать и для определения выбраковочного размера детали, с тем, чтобы отобрать при частичное ремонте детали, которые не­обходимо отремонтировать в мастерской и детали, которые будут ремонтироваться в эксплуатации.

Из зависимости

U=at^b

находим при t = To+T₁+T₂ (время соответствующее частичному ремонту) и U=Uпр.

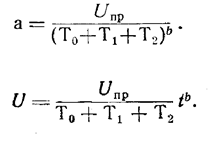
Подставим t = To+T₁ - время профилактики. Имеем для допустимого значения

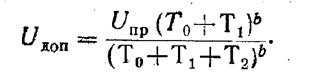
При U>Uдon деталь ремонтируется. При U<Uдоп остается в эксплуатации.

На практике часто вместо определения остаточного ресур­са элемента решают задачу установления возможности оста­вить элемент без замены (профилактики) при заданной на­работке до следующего контроля T₁+Тост. В качестве кри­терия используется экономический критерий, который состоит в следующем. Вероятные удельные издержки, вызванные устранением отказа в эксплуатации, за период от T₁ до T₁+Т^(к)_ост, равные С_Э, и профилактикой (ремонтом) в мастерской в момент T₁+ Т^(к)_ост, равные См, должны быть меньше

удельных издержек на профилактику (ремонт) См в мо­мент T₁.

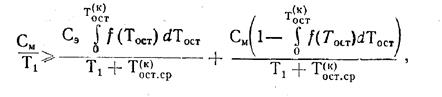
где

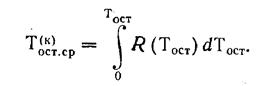
Иначе говоря изделия тогда можно оставлять без профилак­тики (ремонта), если удельные затраты в момент T₁ больше тех, которые предстоит произвести, если изделие откажет в эксплуатации раньше ожидаемого срока или придется вы­полнить ремонт (профилактику) в момент T₁+ Т^(к)_ост.

Задав плотность распределения остаточного ресурса нор­мальным законом с параметрами Т = Т_{ост ср} , σ = νТ_{ост- ср} получим

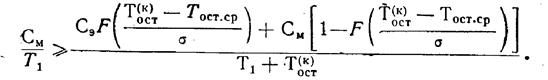
Пример. Определить имеется ли экономическая целесообразность при прогнозировании то реализации, оставлять транспортер с параметрами предыдущего примера (который был диагностирован при T₁=210 сут) без ремонта на время равное минимальному гарантированному остаточному ресурсу.

Поскольку α =0,9, то, следовательно, вероятность того, что транспортер откажет до Т_{ост. гар} равна 0,1, а после него 0,9.

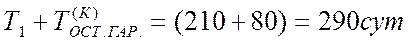
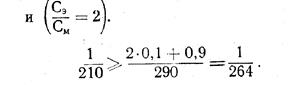
Таким образов, условие экономической целесообразности выполнено и транспортер можно не ремонтировать, а следующую проверку необходимо провести при Т ≈ 300 сут

Для удобства прогноза на некоторый заданный период удобно использовать прогнозирующие графики. Построение графика на примере прямолинейной реализации диагностического параметра и прогноза на один сезон показано на рис. 12.

График строится следующим образом. Реализации продлеваются до встречи с предельным значением, а затем вычитается отрезок равный времени прогноза (в данном случае один сезон). Опуская из полученной точки перпендикуляр до встречи с реализацией находим границу, ниже которой находится область продолжения работы (изделие проработает более одного сезона), а выше—область браковки (изделие не проработает сезон).

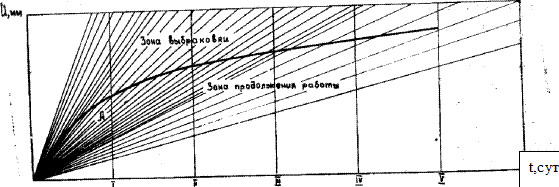
Рис. 12. Прогнозирующие графики для прогноза на один сезон.

Аналогично можно построить области приемки и брака для реализации любого вида.

Процесс прогнозирования с помощью построенных графиков, как видим, существенно упрощается.