Элементы линейной алгебры и аналитической геометрии

Пример 1.1.Заданы матрицы 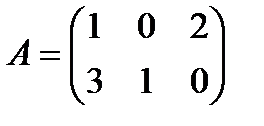, , 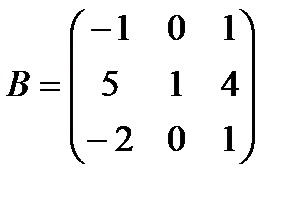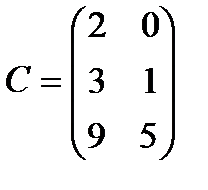. Вычислить:

.

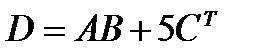Решение.1. Вычислим произведение матриц 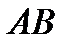. Найдем размерность матрицы-произведения, если умножение заданных матриц возможно: 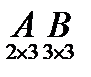. Результатом вычисления будет матрица размера .

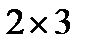Вычислим элементы матрицы-произведения, умножая элементы каждой строки матрицы 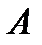на соответствующие элементы столбцов матрицы 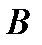следующим образом:

.

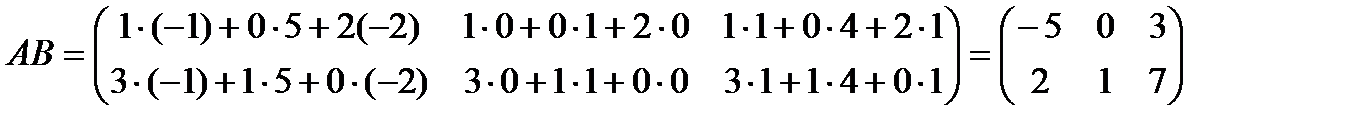2. Найдем матрицу 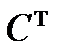. При транспонировании строки и столбцы матрицы 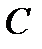меняются местами с сохранением порядка:

.

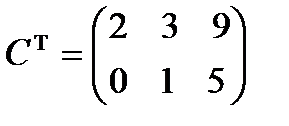3. Умножим матрицу 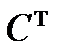на число 5, при этом каждый элемент матрицы умножается на это число:

.

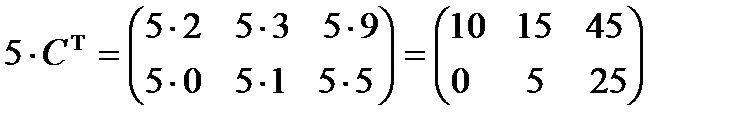4. Вычисляем матрицу :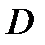

.

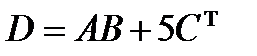
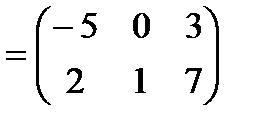
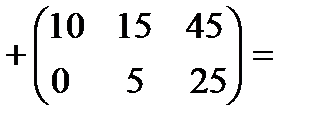
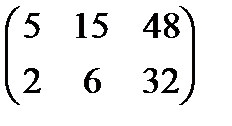Пример 1.2.Решить систему линейных алгебраических уравнений:

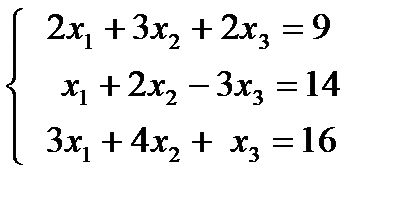
1) методом обратной матрицы; 2) методом определителей (методом Крамера); 3) методом Гаусса.

Решение. 1.Метод обратной матрицы.

Введем обозначения:

, , .

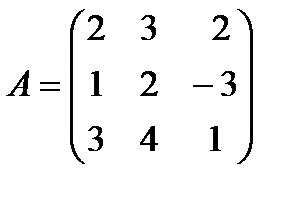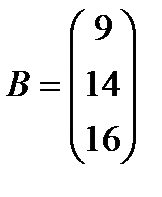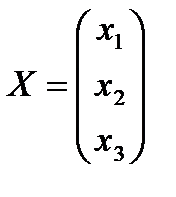Тогда в матричной форме данная система имеет вид: 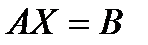. Умножим слева обе части матричного равенства на обратную матрицу 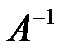, получим 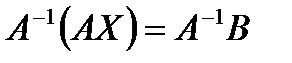. Так как 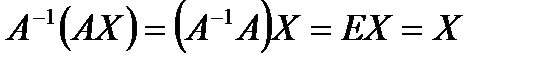, то решением системы методом обратной матрицы будет матрица-столбец

.

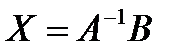(1.1)

Найдем матрицу .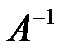

Вычислим определитель матрицы А, применяя, например, формулу

.

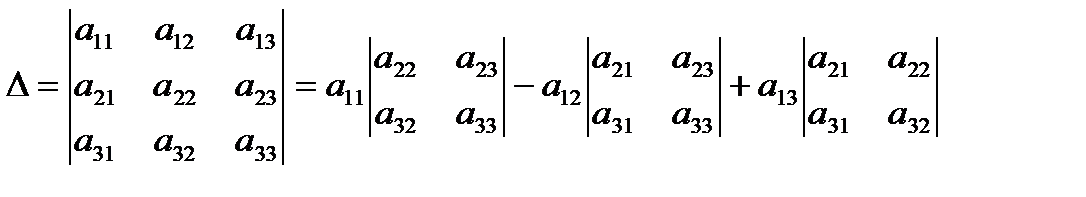(1.2)

,

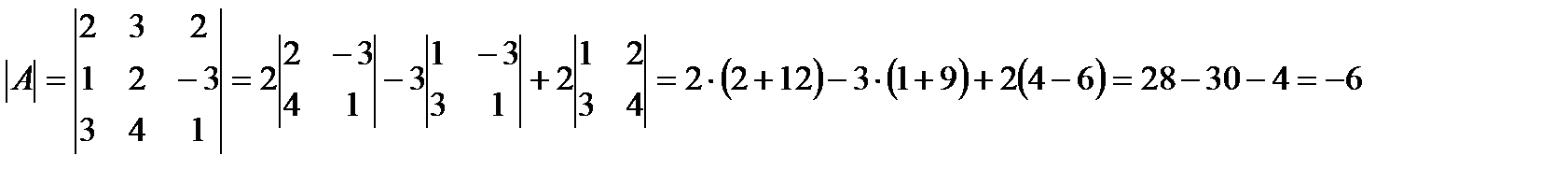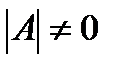, следовательно, обратная матрица 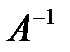существует.

Вычисляем алгебраические дополнения ко всем элементам матрицы :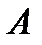

, , ,

, , ,

, , .

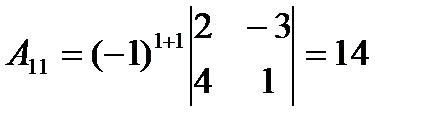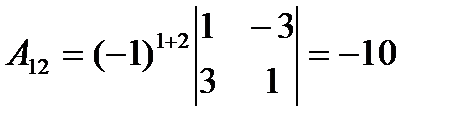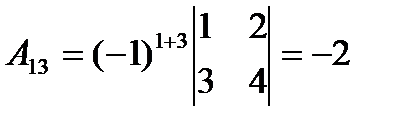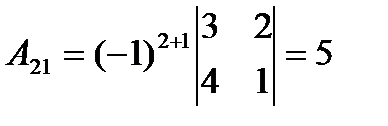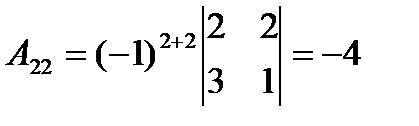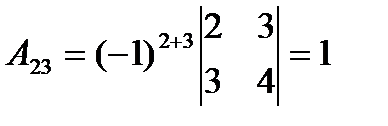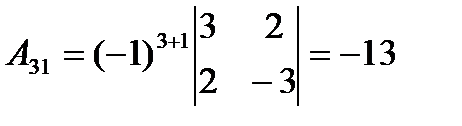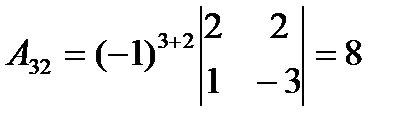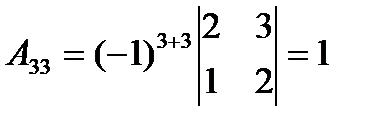Составляем матрицу :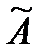

.

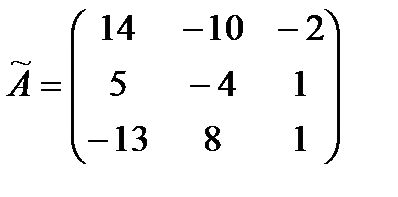Транспонируем матрицу :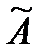

.

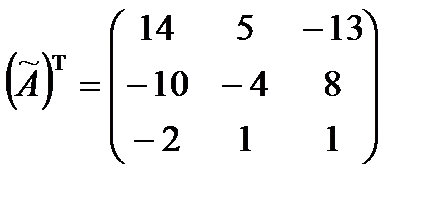Находим обратную матрицу:

.

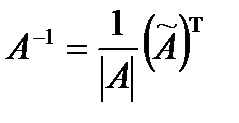
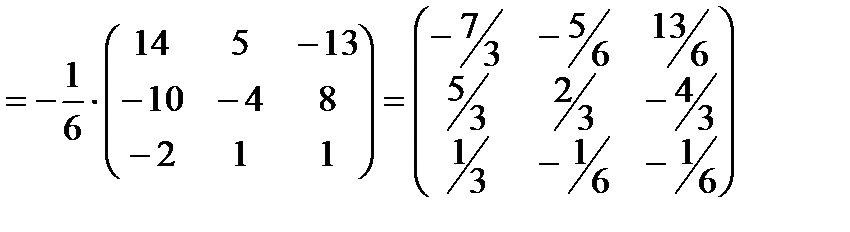Тогда по формуле (1.1)

,

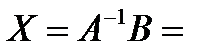
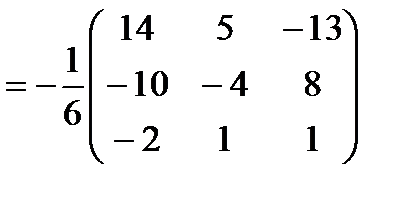
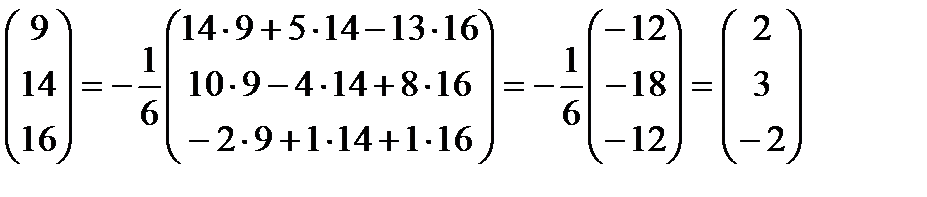то есть решение системы: .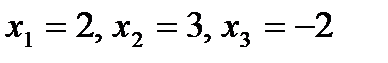

2.Метод определителей (метод Крамера).

Найдем определитель системы 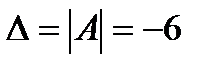(см. п. 1). Так как 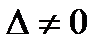, то по теореме Крамера система имеет единственное решение.

Вычислим определители матриц 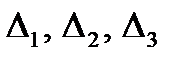, полученных из матрицы 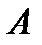, заменой соответственно первого, второго и третьего столбцов столбцом свободных членов:

, , .

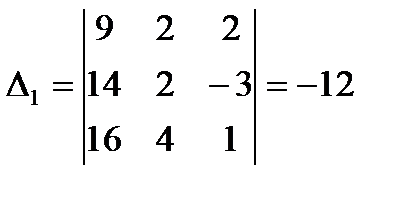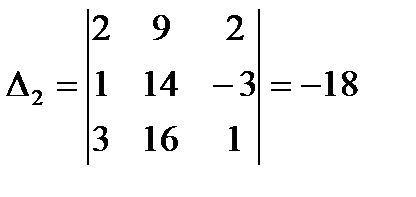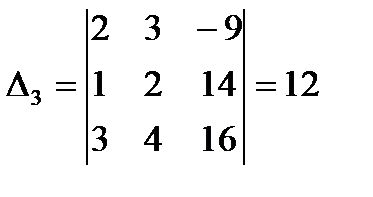Решение системы находим по формулам:

, , ,

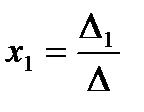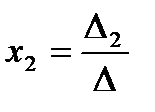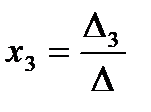откуда получаем

.

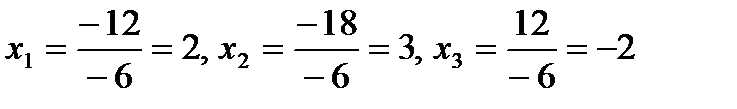3.Метод Гаусса.

Замечание 1.1. Напомним, что метод Гаусса заключается в том, что с помощью элементарных преобразований система уравнений приводится к равносильной системе ступенчатого (или треугольного) вида, из которой последовательно, начиная с последних (по номеру) переменных, находятся все остальные переменные.

Преобразования Гаусса удобнее проводить не с самими уравнениями системы, а с матрицей их коэффициентов, то есть со строками расширенной матрицы системы.

К элементарным преобразованиям относятся:

1) перестановка местами двух строк матрицы;

2) умножение всех элементов строки на число, отличное от нуля;

3) прибавление к элементам одной строки соответствующих элементов другой строки, умноженных на одно и то же число.

Расширенная матрица исходной системы имеет вид

.

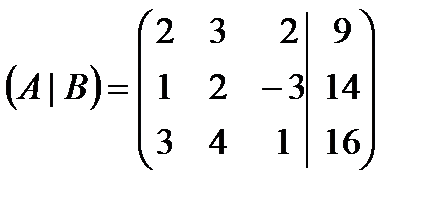Для удобства преобразований, поменяем в расширенной матрице первую и вторую строки:

.

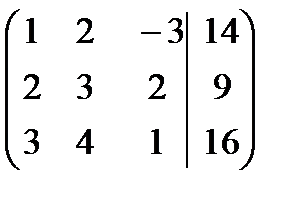Далее умножаем первую строку на 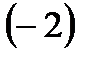и прибавляем ко второй строке, потом умножаем первую строку на 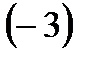и прибавляем её к третьей строке. Третью строку полученной матрицы поделим на :

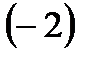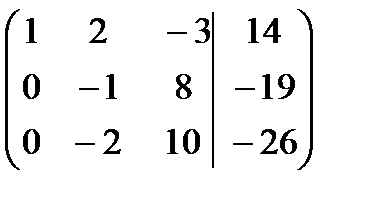
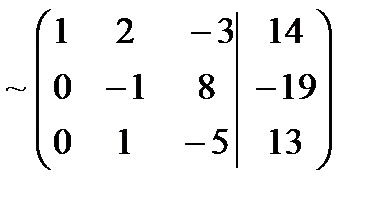
Вторую строку последней матрицы прибавляем к третьей, в результате получим

.

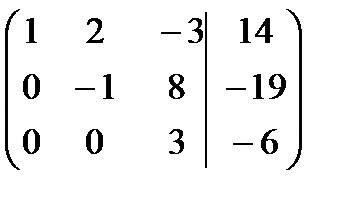Запишем систему уравнений, соответствующую преобразованной матрице коэффициентов:

.

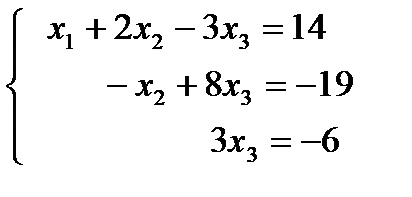Из последнего уравнения находим 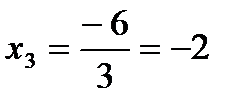; подставляем найденное значение 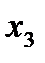во второе уравнение системы: 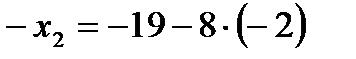, , 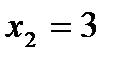и из первого уравнения: , .

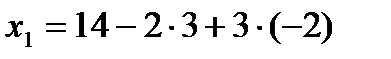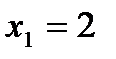Таким образом, решение системы: .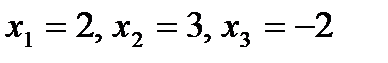

Задача 1. Решить систему линейных алгебраических уравнений: 1) методом обратной матрицы; 2) методом определителей; 3) методом Гаусса.

1.1.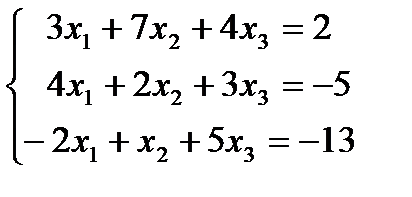	1.2.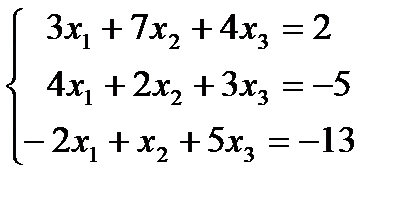
1.3.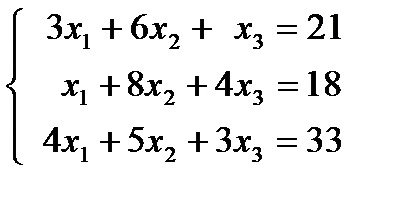	1.4.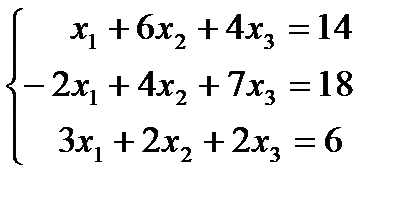
1.5.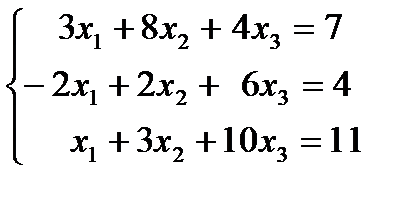	1.6.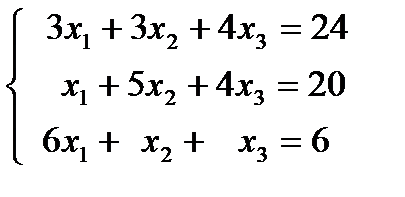
1.7.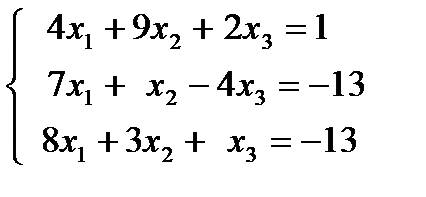	1.8.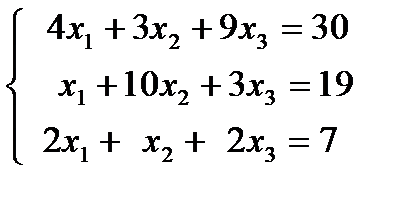
1.9.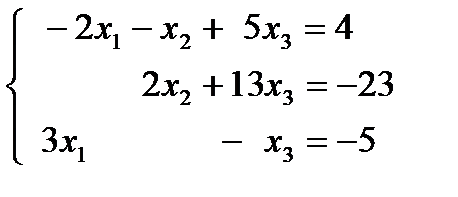	1.10.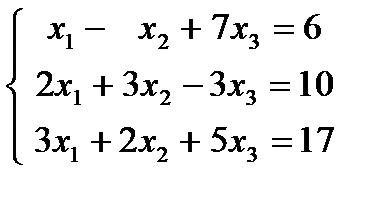
1.11.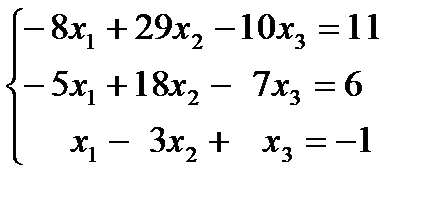	1.12.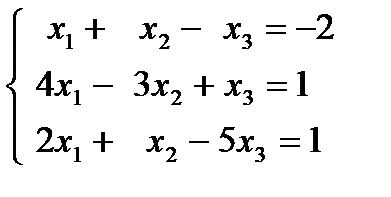
1.13.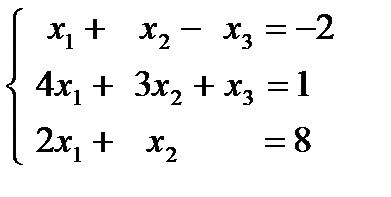	1.14.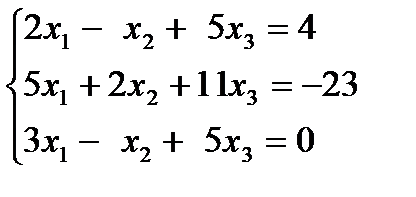
1.15.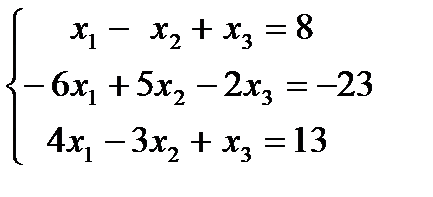	1.16.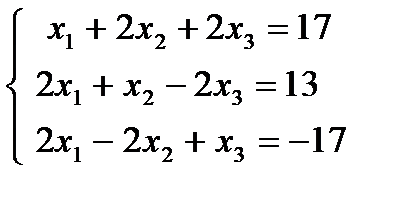
1.17.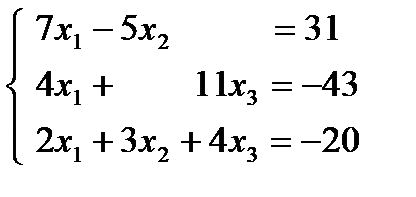	1.18.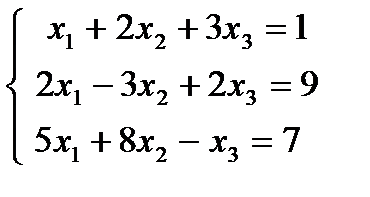
1.19.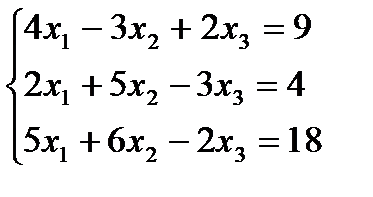	1.20.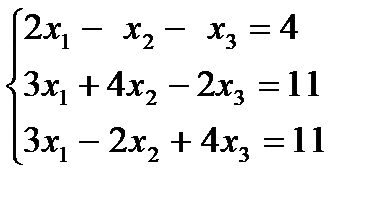
1.21.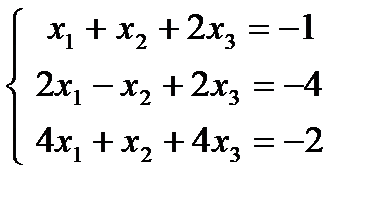	1.22.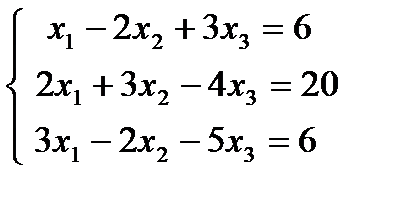
1.23.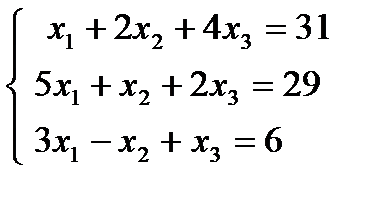	1.24.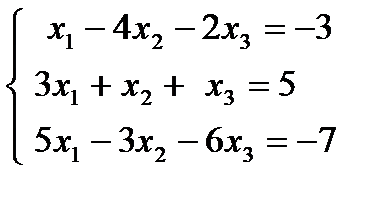
1.25.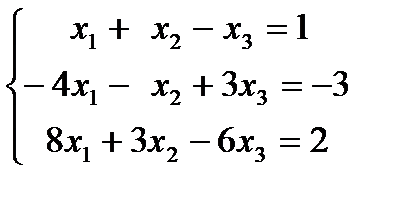	1.26.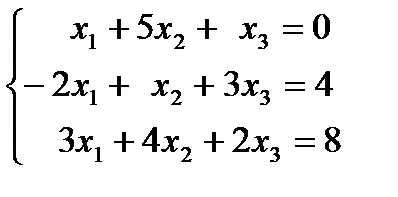
1.27.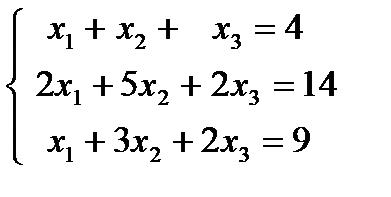	1.28.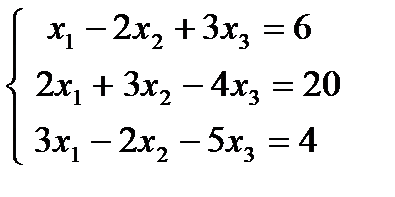
1.29.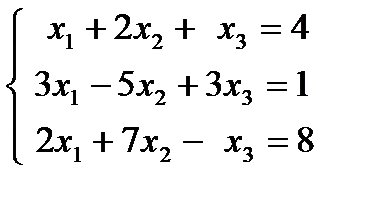	1.30.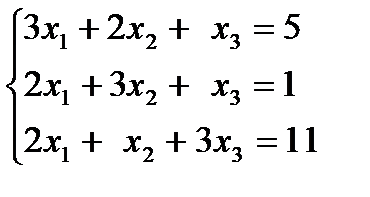

2. ЛИНЕЙНЫЕ ЭЛЕКТРИЧЕСКИЕ ЦЕПИ ПОСТОЯННОГО ТОКА