Законы Ома, Кирхгофа и закон сохранения энергии
Под напряжением на некотором участке электрической цепи понимают разность потенциалов между крайними точками этого участка. Пусть имеется некоторый участок цепи (рис.1.3), крайние точки которого обозначены буквами а и b.
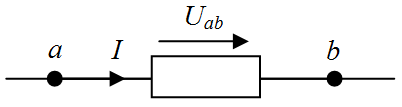
Рис. 1.3 Участок электрической цепи между точками а и b
Пусть ток I течет от точки а к точке b (от более высокого потенциала к более низкому). Следовательно, потенциал точки а (φa) выше потенциала точки b (φb) на значение, равное произведению тока I на сопротивление R:
| φa = φb + IR. |
В соответствии с определением напряжение между точками а и b
| Uab = φa - φb. |
Напряжение Uab = IR на сопротивлении равно произведению тока, протекающего по сопротивлению, на значение этого сопротивления.
В электротехнике разность потенциалов на концах сопротивления принято называть либо напряжением на сопротивлении, либо падением напряжения. Положительное направление падения напряжения на каком-либо участке (направление отсчета этого напряжения), указываемое на рисунках стрелкой, совпадает с положительным направлением отсчета тока, протекающего по данному сопротивлению.
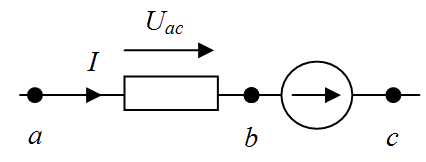
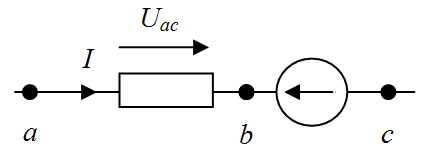
Рассмотрим вопрос о напряжении на участке цепи, содержащей кроме сопротивления R, ЭДС Е (рис. 1.4, а, б). Найдем разность потенциалов (напряжение) между точками а и с для этих участков. По определению Uaс = φa - φс. Выразим потенциал точки а через потенциал точки с. При перемещении от точки с к точке b встречно направлению ЭДС Е (см. рис. 1.4, а) потенциал точки b оказывается меньше, чем потенциал точки с, на значение ЭДС Е: φb = φc - E. При перемещении от точки с к точке b согласно направлению ЭДС Е (рис.1.4, б) потенциал точки b больше, чем потенциал точки с, на значение ЭДС: φb = φc + E.
Так как ток течет от более высокого потенциала к более низкому, то в обеих схемах потенциал точки а выше потенциала точки b на величину падения напряжения на сопротивлении R: φа = φb + IR.
| 
|
| а) | б) |
| Рис. 1.4. Участок цепи, содержащий R, ЭДС Е: потенциал точки b меньше, чем потенциал точки с, на значение ЭДС (а); потенциал точки b больше, чем потенциал точки с, на значение ЭДС (б) |
Таким образом, для рис. 1.4, а:
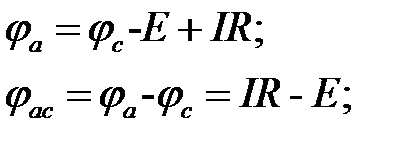
| (1.9) |
для рис. 1.4, б:
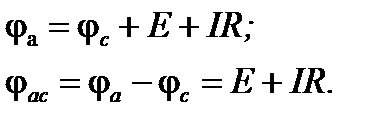
| (1.10) |
Положительное направление напряжения Uaс показывают стрелкой от а к с. Согласно определению, Uса = φс - φа, поэтому Uас = -Uса, т.е. изменение чередования индексов равносильно изменению знака этого напряжения. Следовательно, напряжение может быть как положительной величиной, так и отрицательной.
Закон Ома для участка цепи, не содержащего ЭДС Е, устанавливает связь между током и напряжением на этом участке. Применительно к рис.1.4
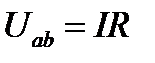 или или 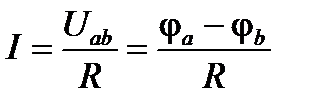 . .
| (1.11) |
Закон Ома для участка цепи, содержащего источник ЭДС Е, позволяет найти ток этого участка по известной разности потенциалов (φa-φс) на концах этого участка цепи и имеющейся на участке ЭДС Е.
Так, из уравнения (1.11) для схемы рис.1.4, а следует
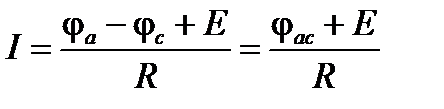
|
Из уравнения (1.11) для схемы рис.1.4, б следует:
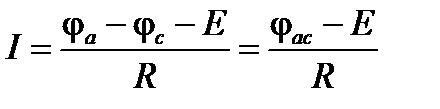
|
В общем случае
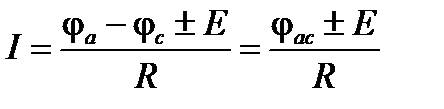 . .
| (1.12) |
Все электрические цепи подчиняются первому и второму законам Кирхгофа.
Первый закон Кирхгофа можно сформулировать двояко (рис.1.5, а):
1) алгебраическая сумма токов, подтекающих к какому-либо узлу схемы, равна нулю;
2) сумма подтекающих к любому узлу токов равна сумме утекающих от этого узла токов.
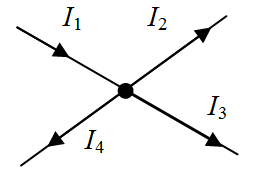
| |
| а) | б) |
| Рис. 1.5. К пояснению первого (а) и второго (б) законов Кирхгофа |
Применительно к (рис.1.5, а), если подтекающие токи к узлу считать положительными, а вытекающие - отрицательными, то согласно первой формулировке I1-I2-I3-I4=0; согласно второй I1=I2+I3+I4. Физически первый закон Кирхгофа означает, что движение электрических зарядов в цепи происходит так, что ни в одном из узлов они не скапливаются. В противном случае изменялись бы потенциалы узлов и токи в ветвях.
Второй закон Кирхгофа также можно сформулировать двояко (рис.1.5, б):
1) алгебраическая сумма падений напряжений в любом замкнутом контуре равна алгебраической сумме ЭДС, входящих в данный контур:
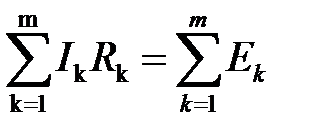 . .
| (1.13) |
где m - число резистивных элементов; п – число ЭДС в контуре (в каждую из сумм соответствующие слагаемые входят со знаком плюс, если они совпадают с направлением обхода контура, и со знаком минус, если они не совпадают с ним);
| SEk = SIiRi, E1-E2+E3 = I1R1+ I2R2+ I3R3+ I4R4. | (1.14) |
Правило: если направление тока и Е совпадает с направлением обхода то в уравнении берётся со знаком «+», если не совпадает, то «-».
2) алгебраическая сумма напряжений вдоль любого замкнутого контура (рис.1.5, б)
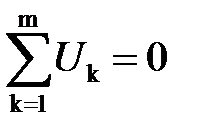 , ,
| (1.15) |
где т - число элементов контура.
Законы Кирхгофа справедливы для линейных и нелинейных цепей при любом характере изменения во времени токов и напряжений.
Баланс мощностей
При протекании токов по сопротивлениям в них выделяется теплота. На основании закона сохранения энергии количество теплоты, выделяющееся в единицу времени в сопротивлениях цепи, должно равняться энергии, доставляемой за то же время источником питания. Если направление тока I, протекающего через источник ЭДС E, совпадает с направлением ЭДС, то источник ЭДС доставляет в цепь энергию в единицу времени, равную EI, и произведение ЕI входит в уравнение энергетического баланса с положительным знаком. Если же направление тока I встречно ЭДС Е, то источник ЭДС не поставляет энергию, а потребляет ее (например, заряжается аккумулятор), и произведение ЕI войдет в уравнение энергетического баланса с отрицательным знаком. Уравнение энергетического баланса при питании только от источников ЭДС имеет вид
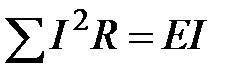 . .
| (1.15) |
В случае питания электрической цепи не только источниками ЭДС, но и источниками тока, при составлении уравнения энергетического баланса необходимо учесть и энергию, доставляемую источниками тока. Предположим, что к узлу а схемы подтекает ток J от источника тока, а от узла b этот ток утекает. Доставляемая источником тока мощность равна UаbJ. Общий вид уравнения энергетического баланса:
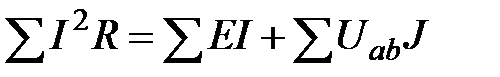 . .
| (1.16) |
Дата добавления: 2021-12-14; просмотров: 592;











