Решение систем линейных уравнений

Векторные и матричные операторы и функции системы Mathcad позволяют решать задачи линейной алгебры.

Например, решим следующую систему линейных уравнений:

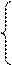4*x1+0.24*x2-0.08*x3=8

0.09*x1 + 3*x2-0.15*x3=9

0.04*x1 -0.08*x2+ 4*x3=20

Возможны 2 способа решения систем:

I. Для решения системы линейных уравнений матричным способом необходимо:

1. Задать матрицу А коэффициентов системы.

2. Задать вектор В свободных членов системы.

3. Задать вектор X решения системы уравнения матричными операторами.

4. Вывести результаты решения.

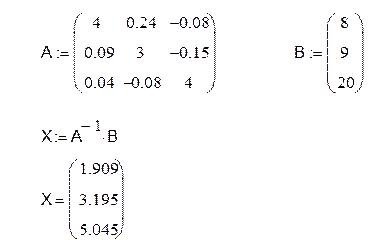В матричной форме А*Х:=В, где

Х1 Х2 Х3

Х- вектор решения линейных уравнений.

Результат решения системы

линейных уравнений (относительно x1, x2, x3)

II. Для решения системы линейных уравнений с помощью функции lsolve(A,B) необходимо:

1. Задать матрицу А коэффициентов системы.

2. Задать вектор В свободных членов системы.

3. Задать вектор X1 решения системы уравнения с помощью функции lsolve().

4. Вывести результаты решения.

Результат решения

системы линейных уравнений

После решения системы необходимо сделать проверку полученных корней, путем подстановки их в уравнения. Например,

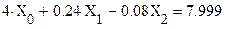С погрешностью 0,0001 результат совпал.

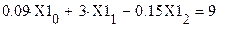Вывод: корни найдены правильно.

8.1. Решение нелинейных уравнений

Многие уравнения, такие как трансцендентные, и системы нелинейных уравнений не имеют аналитических решений. Они могут решаться численными методами с заданной погрешностью (< 0.0001).

Поиск корня с помощью функции root()

Для решения уравнения вида F(x)=0 предназначена функция:

root(выражение, имя переменной)

Функция ищет один корень в окрестности начального значения, которое должно быть предварительно задано. Если решения нет, то надо изменить начальное значение. Для его выбора можно нарисовать график.

Если корней много, то после нахождения очередного корня выражение можно упростить, исключая корень x_i делением выражения на (x-x_i). Для нового выражения можно искать очередной корень.

Пример вычисление корней кубического полинома

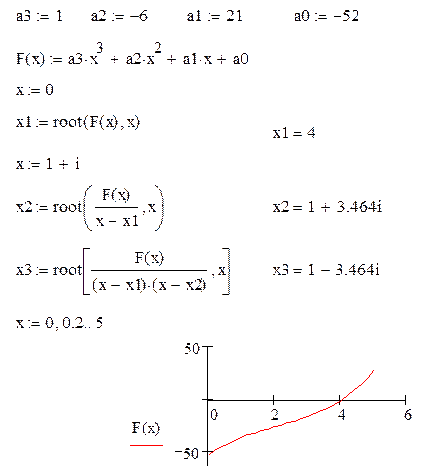Коэффициенты полинома

Задано выражение

Начальное значение

Поиск первого корня

Новое начальное значение

Исключение первого корня

Поиск второго корня

Исключение 1-го и 2-го корней

Поиск третьего корня

Ранжированная переменная

График функции для уточнения

начальных значений.

Поиск корня с помощью символьных вычислений

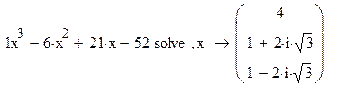Ввод шаблона с ключевым словом

solve (решить), заполнение маркеров

выражением и переменной и вывод

расчета корней в векторном виде.

Вычисление корней полиномиального уравнения с помощью функции polyroots

Для поиска корней полинома степени n предназначена функция:

polyroots(V)

Она возвращает вектор корней многочлена (полинома) степени n, коэффициенты которого находятся в векторе V имеющем длину равную n+1. Коэффициенты должны располагаться в векторе в порядке увеличения степеней (начиная с a0).

Корни полинома могут быть как вещественными, так и комплексными числами.

Функция ищет сразу все корни полинома.

Не рекомендуется пользоваться этой функцией при n > 5…6, при этом точность вычисления невысока.

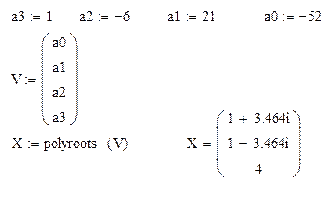Коэффициенты полинома

Они же в форме вектора V

Поиск и вывод корней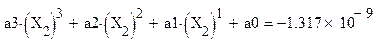

.

Проверка решения уравнения относительно 3-го корня дает с учетом погрешности < < 0.00001 весьма точный результат, т.е. ответ ® 0.

8.2. Решение системы нелинейных уравнений

При решении систем нелинейных уравнений используется специальный вычислительный блок, открываемый служебным словом – директивой Given и имеющий следующую структуру:

Given

Уравнения

Ограничительные условия

Выражения с функциями Find или Minerr. Они используют разные алгоритмы.

Между этими функциями существуют принципиальные различия.

Find(v1,v2,…,vn) – возвращает значение одной или нескольких переменных

для точного решения (решение реально существует);

Minerr(v1,v2,…,vn) - возвращает значение одной или нескольких переменных

для приближенного решения (решение может не существовать, находится минимальная среднеквадратичная погрешность к окрестности существования корней или минимального сближения).

Эти функции могут применяться только после блока Given. Имена этих функций можно писать и строчными буквами. При вводе ограничительных условий необходимо использовать логические операторы: >, <, ³, £, ¹, =.

Функции Find и Minerrмогут использоваться для решения как одного, так и ряда уравнений. Рекомендуется после нахождения решения сделать проверку подстановкой.

Пример решения системы двух уравнений с ограничениями.

Заданы два уравнения y=x² и y= 8+3*x.

Найдём первое решение при ограничении x<0.

x:=0 y:=0 Начальные значения

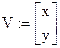То же в векторной форме

Given Начало блока

y=x² Уравнение 1 (парабола)

y=8+3x Уравнение 2 (прямая)

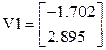x<0 Ограничения на х

V1:=Find(x,y) Первое решение. Прямая и парабола

пересекаются в точке x1= –1,702 и y1=2,895

Найдём второе решение при ограничении x>0.

x:=3 y:=20 Начальные значения

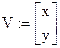То же в векторной форме

Given Начало блока

y=x² Уравнение 1 (парабола)

y=8+3x Уравнение 2 (прямая)

x>0 Ограничения на х

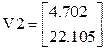V2:=Minerr(x,y) Второе решение. Прямая и парабола

пересекаются в точке x2=4,702 и y2=22,105

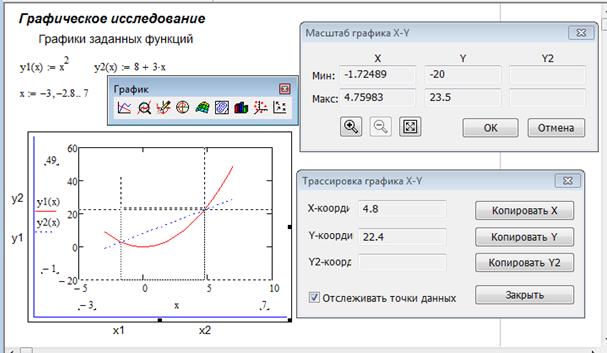
Рассмотрим пример решения системы 2 нелинейных уравнений средствами Mathcad.

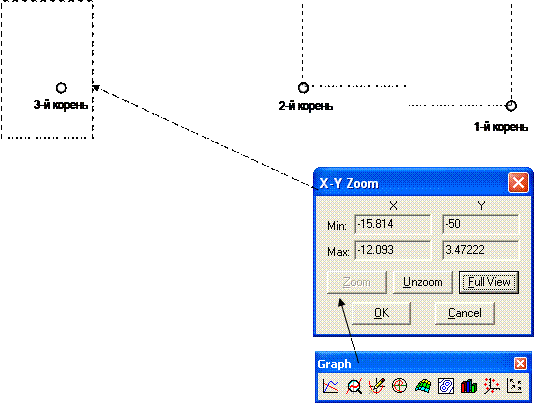
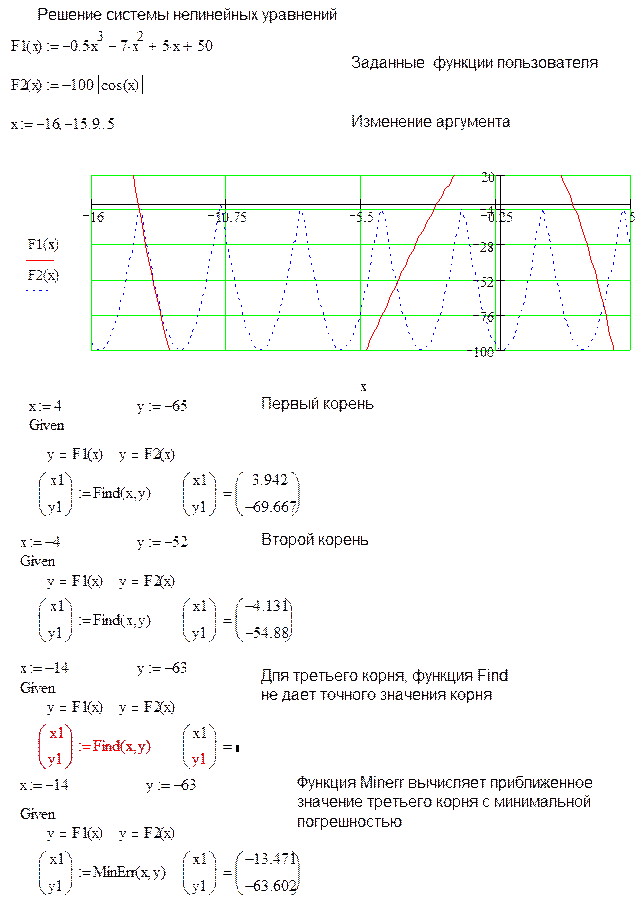
С помощью окна масштаб можно изменить диапазон значений, отображаемых на графике для исследования характера изменения функции в критических точках.