Статическая определимость механизма как объекта силового расчета.

При решении задач силового расчета любой механической системы прежде всего необходимо выяснить вопрос о статической неопределимости системы. В любом механизме одно звено неподвижно и оно находится в равновесии вне зависимости от сил, приложенных к этому звену. Таким образом, силовой анализ системы сводится к рассмотрению равновесия п подвижных звеньев механизма, для которых, в случае плоского движения, можно составить 3п уравнений равновесия (см. курс ТМ). Если установлены все внешние силы, действующие на звенья механизма, то искомыми остаются реакции в кинематических парах, классификация которых определяет число неизвестных в упомянутых уравнениях равновесия.

В представленных в Задании на проект механизмах звенья в форме стержней и ползуны объединены в кинематическую цепь кинематическими парами V класса, вращательными и поступательными. Вращательная пара представлена цилиндрическим шарниром, для которого известна точка приложения реакции, но эта реакция неизвестна ни по модулю, ни по направлению; поступательная пара представлена ползуном и его направляющей, и реакция в этой паре известна по направлению

(это направление перпендикулярно направляющей), но неизвестны модуль реакции и точка ее приложения. Таким образом, получаем, что число неизвестных в системе из 3п уравнений равновесия механизма равно 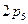( — число кинематических пар пятого класса). 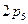В результате условие статической определимости механизма определится следующим соотношением между числом подвижных звеньев и числом кинематических пар V класса: 3п = или .

Данное соотношение совпадает с формулой, устанавливающей соотношение между числом звеньев и кинематических пар V класса для группы Ассура и используемой для классификации этих групп. В результате делаем вывод: группа Ассура является статически определимой группой звеньев, поэтому может быть выбран следующий порядок силового анализа механизма: разложить кинематическую цепь механизма на группы Ассура, выполнить силовой расчет каждой группы отдельно, выполнить силовой расчет начального звена и обобщить полученные результаты.

Замечание.Попытки определения реакций в кинематических парах механизма путем рассмотрения равновесия отдельных его звеньев приводят обычно к статически неопределимым расчетным схемам. Например, если выделить звено, образующее со смежными звеньями две вращательные кинематические пары V класса, то в трех уравнениях равновесия этого звена имеем четыре неизвестные: модули и направления реакций в парах. Поэтому силовой расчет отдельного звена возможен лишь в заключительной стадии анализа группы, когда некоторые реакции уже известны, либо когда направление какой-либо реакции заранее известно.

Последовательность силового расчета структурных групп обратна последовательности их присоединения к начальному звену. Это обусловлено определенностью системы сил, действующих на последнюю в структуре механизма группу звеньев, поскольку данная группа включает выходное звено, нагрузочная характеристика которого обычно является заданной. Иная последовательность приводит к статически неопределимым расчетным схемам, поскольку для промежуточной группы неизвестной остается сила, действующая на звенья данной группы со стороны звеньев последующей в порядке «наслоения» (см. выше) группы.

В Задании на курсовой проект последние в структуре всех механизмов группы представлены одним типом — группой II класса 2-го порядка второго вида, поэтому изложение метода кинетостатики в силовом анализе механизма начинаем именно с этой группы. Промежуточные группы могут быть представлены также группами других видов, силовой анализ которых приведен ниже.