Цель и задачи кинематического анализа
Цель кинематического анализа — изучение кинематических характеристик механизма: траекторий движения, скоростей и ускорений характерных точек и звеньев механизма. В ходе анализа решаются следующие исследовательские задачи:
- определяются положения механизма в различные моменты времени его установившегося движения; выполняется построение траектории заданной точки механизма;
- выполняется кинематический анализ механизма методом планов: выполняется построение планов скоростей и ускорений, вычисляются скорости и ускорения
характерных точек механизма (кинематических пар, центров масс звеньев), а также угловых скоростей и ускорений звеньев механизма в различных его положениях;
- выполняется кинематический анализ механизма методом диаграмм: составляется функция перемещения выходного звена механизма в зависимости от обобщенной координаты (втабличной и графической формах); методом графического дифференцирования строятся диаграммы аналогов скоростей и аналогов ускорений выходного звена; по значениям аналогов вычисляются значения скоростей и ускорений выходного звена в функции времени;
- выполняется сравнительный анализ результатов кинематического анализа методом планов и методом диаграмм.
Решение первой из этих задач позволит установить ход звеньев (что даст возможность определить очертания контура машины), выяснить соответствие движения звеньев правильной последовательности реализуемых процессов. Решение другой задачи позволит оценить кинематику механизма с точки зрения её соответствия установленным регламентным ограничениям (например, ограничениям скорости подачи режущего инструмента в исполнительных механизмах рабочих машин). Кроме того, результаты кинематического анализа используются при исследовании динамики машины — в частности, при определении приведенных к начальному звену механизма силовых и инерционных характеристик, при силовом анализе механизма.
3.2. Построение плана положений механизма
Исходными данными для решения данной задачи являются:
1) кинематическая схема механизма;
2) закон движения входного (ведущего) звена.
В задании к РГР приведены эскиз механизма и исходные данные для построения его кинематической схемы. Согласно заданию, закон движения входного звена (в проекте анализируются кривошипные механизмы) представлен постоянной угловой скоростью кривошипа, поэтому наиболее удобным представляется построение кинематической схемы механизма через равные промежутки времени в пределах одного цикла установившегося движения. Поскольку для всех вариантов механизмов, представленных в задании, цикл движения механизма соответствует одному обороту ведущего звена — кривошипа 1, то получаем: через равные промежутки времени кривошип занимаетугловые положения, равномерно распределенные в пределах
3600— полного угла поворота кривошипа.
Таким образом, построение плана положений механизма начинается с построения положений ведущего звена — кривошипа (количество этих положений при курсовом проектировании обычно принимается в пределах от 6 до 12). Отсчет положений осуществляется от начального (нулевого) положения, которое выбирается, исходя из следующего.
В исполнительных механизмах представленного в задании на проект типа (преобразующих непрерывное вращательное движение в возвратно-поступательное) начальное (нулевое) положение звеньев механизма обычно выбирается из двух крайних его положений, а именно то положение, которое соответствует началу рабочего хода выходного звена — ползуна. В технологических машинах (например, в строгальном станке) на этом ползуне, совершающем возвратно-поступательное движение, может быть закреплен режущий инструмент; в транспортных машинах (например, в качающемся конвейере) ползун может перемещать какие-то объекты и т д. В фазе рабочего хода к ползуну приложена сила производственного сопротивления, направленная против движения ползуна и совершающая, таким образом, отрицательную работу. В результате направление этой силы и определит выбор начального положения механизма из двух крайних.
Операция отыскания крайних положений звеньев выполняется исходя из вида структурных групп механизма и начинается с определения крайних положений звеньев группы, которая присоединена к начальному механизму, образованному ведущим звеном и стойкой. Пусть, например, к начальному механизму присоединена группа IIкласса 2-го порядка первого вида (см. рис. 3.1, а), образующая (вместе с начальным механизмом) кривошипно-коромысловый механизм.
Коромысло 3 будет занимать крайнее правое положение, когда кривошип 1 и шатун 2 будут располагаться на одной прямой так, как показано на рис.3.1, б. При этом кинематическая пара С будет наиболее удалена от центра вращения кривошипа А и это её положение определится точкой пересечения двух дуг: радиусом (АВ + ВС) и радиусом СD. Коромысло 3 будет занимать крайнее левое положение, когда кривошип 1 и шатун 2 будут также располагаться на одной прямой, но другим образом — так, как показано на рис.3.1, в. При этом кинематическая пара С будет наиболее приближена к центру вращения кривошипа и это её положение определится точкой пересечения двух дуг: радиусом (ВС − АВ) и радиусом СD.
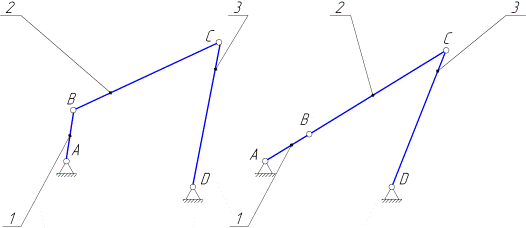
а) б)
в)
Рис. 3.1
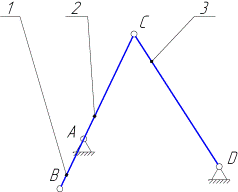
Другим характерным примером является присоединение к начальному механизму группы II класса 2-го порядка третьего вида (см. рис. 3.2, а), образующая (вместе с начальным механизмом) кривошипно-кулисный механизм.
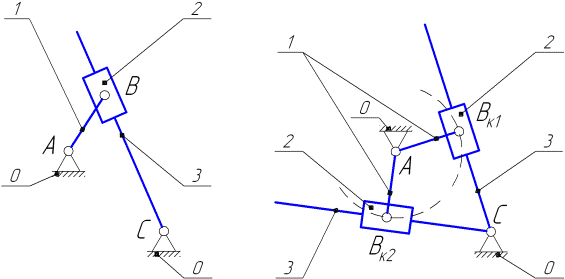
а) б)
Рис. 3.2
Ось кулисы 3 в крайних её положениях будет занимать положения касательных к окружной траектории движения концевой точки кривошипа — вращательной кинематической пары В, с которой геометрически совпадает поступательная пара — центральная пара структурной группы 2,3 (см. рис.3.2, б). Определение крайних положений структурных групп, последовательно присоединяемых к рассмотренным механизмам, выполняется согласно тем же принципам.
Следующий этап рассматриваемой задачи — выбор направления вращения кривошипа 1. В этой связи используем понятия фазовых углов поворота кривошипа. Угол поворота кривошипа, при котором происходит перемещение выходного звена из одного крайнего положения в другое, называется фазовым углом. Если при таком перемещении на выходное звено действует сила производственного сопротивления, то соответствующий фазовый угол называется фазовым углом рабочего хода; если при данном перемещении сила производственного сопротивления отсутствует, то соответствующий фазовый угол называется фазовым углом холостого хода.
Фазовые углы обычно отличаются друг от друга и при перемене направления вращения кривошипа взаимно обратимы. Отсюда следует, что при постоянной скорости вращения кривошипа время рабочего хода может существенно отличаться от времени холостого хода. Поэтому выбор указанного направления определяется требуемыми характеристиками движения выходного звена в фазе рабочего хода. Если скорость выходного звена ограничена сверху (например, в металлорежущих станках), то направление вращения кривошипа выбирается таким образом, чтобы фазовый угол рабочего хода был больше фазового угла холостого хода; если требуются высокие скорости и ускорения движения выходного звена в фазе рабочего хода, то принимается обратное решение. В прилагаемых к настоящему Пособию примерах выполнения курсового проекта операция выбора направления вращения кривошипа проиллюстрирована достаточно полно.
После определения начального положения и выбора направления вращения входного звена — кривошипа — выполняется собственно построение плана положений механизма через равные углы поворота входного звена. Построение плана осуществляется методом «геометрических мест», сущность которого рассмотрим на примере построения плана положений кривошипно-коромыслового механизма.
Пусть начальным положением механизма является положение, в котором кривошип 1 и шатун 2 располагаются на одной прямой так, как показано на рис. 3.3(начальное положение выделено жирными линиями). Пусть также выбрано направление вращения кривошипа против часовой стрелки.
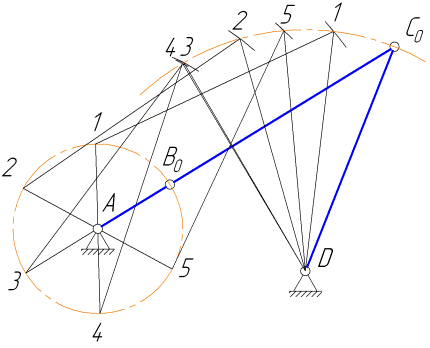
Рис. 3.3
Согласно упомянутому методу, из центра цилиндрического шарнираА строим окружность радиусом АВ— геометрическое место положений шарнира В(концевой точки кривошипа 1). Будем строить положения механизма через каждые 60 градусов поворота кривошипа, поэтому разбиваем окружность на шесть равных частей и получаем точки 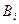 (на рисунке по окружности расположены цифровые индексы точек
(на рисунке по окружности расположены цифровые индексы точек 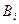 ). Соединяем точки
). Соединяем точки 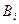 с центромА и строим шесть положений кривошипа.
с центромА и строим шесть положений кривошипа.
Для построения положений шатуна 2 и коромысла 3 определяем положения шарнира С. Из центра шарнира Dпроводим дугу радиусом СD. Получаем первое геометрическое место положений шарнира С. Затем из точек 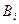 как из центров строим семейство дуг радиусом ВС , получаем второе геометрическое место положений шарнира С. В пересечениях этих двух геометрических мест получаем точки
как из центров строим семейство дуг радиусом ВС , получаем второе геометрическое место положений шарнира С. В пересечениях этих двух геометрических мест получаем точки 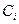 . Соединяем эти точки с точками
. Соединяем эти точки с точками 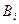 и получаем шесть положений шатуна 2; соединяем точки
и получаем шесть положений шатуна 2; соединяем точки 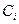 с центром шарнира D и получаем шесть положений коромысла 3. В совокупности получаем шесть положений механизма (см. рис. 3.3).
с центром шарнира D и получаем шесть положений коромысла 3. В совокупности получаем шесть положений механизма (см. рис. 3.3).
На основе плана положений механизма достаточно просто изучаются траектории движения различных точек механизма. Пусть, например, необходимо установить траекторию центра масс звена 2, полагая звено 2 однородным стержнем. Отмечаем срединные точки звена во всех его шести положениях и обводим это семейство точек плавной кривой (выделена на рис. 3.3 пунктирной линией). Полученная кривая является искомой траекторией.
3.3. Кинематический анализ методом планов
3.3.1. Построение планов скоростей
Кинематический анализ механизмов методом планов — графический способ решения уравнений, описывающих кинематические соотношения между скоростями
и ускорениями точек звеньев механизма как твердых тел и выведенных в курсе теоретической механики (ТМ).
Предварительной операцией в построении планов скоростей является определение скорости точки входного звена, в которой к этому звену присоединяется звено первой в структуре механизма группы Ассура. В механизмах, представленных в Задании к курсовому проекту, такой точкой является концевая точкаВ кривошипа, поэтому по заданной угловой скорости вращения кривошипа получаем:
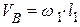 .
.
Направлена скорость точкиВ по касательной к её окружной траектории (т.е. перпендикулярно оси кривошипа) в сторону вращения кривошипа.
Дальнейшее рассмотрение по данной теме ограничим примерами построения планов скоростей для двух структурных групп, приведенных выше.
Пусть к механизму I класса присоединена структурная группа II класса 2-го порядка первого вида (группа 2,3, см. рис. 3.4, а). Необходимо построить план скоростей для группы в некотором промежуточном положении её звеньев.
Известны скорости концевых кинематических пар группы 2,3 — точекВ и D: скорость точки В определена выше, скорость неподвижной точки равна нулю. Найдем скорости других характерных точек группы : шарнира С и центров масс звеньев группы.
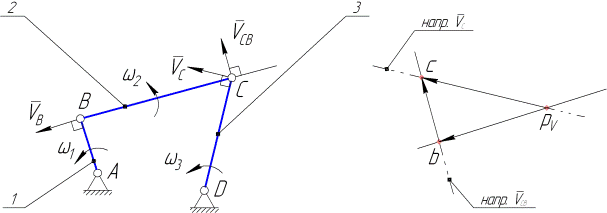
Для отыскания скорости точкиС воспользуемся соотношением, выведенными в курсе ТМ и связывающим скорости двух точек тела при плоском движении последнего. ТочкаС принадлежит звену 2, поэтому, считая точку В полюсом, получаем: 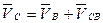 (3.1)
(3.1)
а) б)
Рис. 3.4
В векторном уравнении (3.1)известны величина и направление скорости точкиВ (см. выше), направление скорости точки С в её вращательном движении вокруг не-
подвижной точки D ( 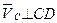 ), направление скорости точкиС в её вращательном
), направление скорости точкиС в её вращательном
движении вокруг точки В ( 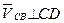 ). Таким образом, в уравнении имеем две неизвестные величины —модули векторов
). Таким образом, в уравнении имеем две неизвестные величины —модули векторов 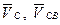 . Графический способ решения уравнения позволяет найти эти неизвестные.
. Графический способ решения уравнения позволяет найти эти неизвестные.
Отмечаем на чертеже произвольную точку 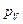 и строим вектор
и строим вектор 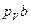 , изображающий в принятом масштабе скорость точки В. Если, например, скорость точки Вравна 5 м/с, а масштаб для изображения скоростей принят равным
, изображающий в принятом масштабе скорость точки В. Если, например, скорость точки Вравна 5 м/с, а масштаб для изображения скоростей принят равным  0,1
0,1 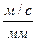 , то длина вектора
, то длина вектора 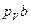 будет равна 50 мм. Направлен вектор
будет равна 50 мм. Направлен вектор 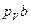 также, как вектор
также, как вектор 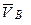 (см. рис. 3.4, б). Согласно уравнению (3.1) с концом вектора
(см. рис. 3.4, б). Согласно уравнению (3.1) с концом вектора 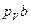 должно быть совмещено начало вектора, изображающего скорость
должно быть совмещено начало вектора, изображающего скорость 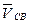 , однако, поскольку известно только направление этого вектора, то возможно лишь построение вспомогательнойпрямой, на которой лежит вектор скорости
, однако, поскольку известно только направление этого вектора, то возможно лишь построение вспомогательнойпрямой, на которой лежит вектор скорости 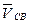 (см. рис. 3.4, б). Вектор скорости
(см. рис. 3.4, б). Вектор скорости 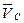 как суммы векторов
как суммы векторов 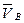 и
и 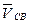 своим началом имеет начало вектора
своим началом имеет начало вектора 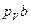 , поэтому возможно построение вспомогательной линии, на которой лежит данный вектор.
, поэтому возможно построение вспомогательной линии, на которой лежит данный вектор.
В пересечении этих двух направлений имеем точку с— конец вектора 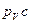 , изображающего на плане скоростей скорость точки С. Отрезок bc определим как вектор, изображающий скорость
, изображающего на плане скоростей скорость точки С. Отрезок bc определим как вектор, изображающий скорость 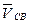 и в результате устанавливаем, что построенный векторный треугольник является непротиворечивым графическим изображением векторного уравнения (3.1). Этот векторный треугольник определим как план скоростей для механизма на рис. 3.4,а). Численные значения неизвестных скоростей найдем непосредственно из плана скоростей, измерив соответствующие отрезки и умножив полученные длины на масштабный коэффициент плана:
и в результате устанавливаем, что построенный векторный треугольник является непротиворечивым графическим изображением векторного уравнения (3.1). Этот векторный треугольник определим как план скоростей для механизма на рис. 3.4,а). Численные значения неизвестных скоростей найдем непосредственно из плана скоростей, измерив соответствующие отрезки и умножив полученные длины на масштабный коэффициент плана:
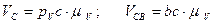 .
.
Значения угловых скоростей звеньев 2, 3 механизма найдём, также используя данные плана скоростей. Скорость  является линейной скоростью точки С как конечной точки звена 3 в его вращательном движении вокруг центра D; скорость
является линейной скоростью точки С как конечной точки звена 3 в его вращательном движении вокруг центра D; скорость  является линейной скоростью точки С как конечной точки звена 2 в его вращательном движении вокруг центра B. Отсюда делаем вывод : искомые угловые скорости вычисляются по известной формуле :
является линейной скоростью точки С как конечной точки звена 2 в его вращательном движении вокруг центра B. Отсюда делаем вывод : искомые угловые скорости вычисляются по известной формуле :
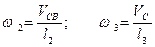 .
.
Направления угловых скоростей определяются направлениями соответствующих линейных скоростей (см. рис. 3.4а).
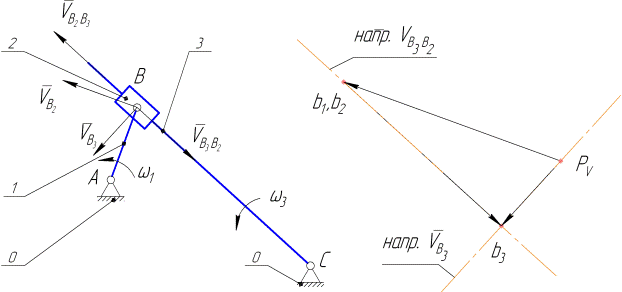
Пусть далее к механизму I класса присоединена структурная группа II класса 2-го порядка третьего вида (группа 2,3, см. рис. 3.5, а). Как и выше, известно движение концевой точки кривошипа – точки  (нижний индекс показывает принадлежность точки В на рисунке звену 1) ; соответственно известно движение ползуна 2 (размерами ползуна пренебрегаем, поэтому его относим к точке
(нижний индекс показывает принадлежность точки В на рисунке звену 1) ; соответственно известно движение ползуна 2 (размерами ползуна пренебрегаем, поэтому его относим к точке  ) - это движение совпадает с движением точки
) - это движение совпадает с движением точки  , т.е. траектории, скорости и ускорения этих точек одинаковы.
, т.е. траектории, скорости и ускорения этих точек одинаковы.
Переходим к определению скоростей точек, принадлежащих кулисе 3. Зафиксируем на кулисе точку В3, геометрически совпадающую в рассматриваемом положении механизма с точками В1, В2, и рассмотрим уравнение, связывающее скорости этих точек. Исходим при этом из того, что движение точки В2можно рассматри-
а) б)
Рис. 3.5
вать как движение двух видов. С одной стороны, движение точки В2 как точки, совпадающей в каждый момент времени с точкой В1, вполне определено (см. выше) - это движение по окружной траектории с центром в точке А. С другой стороны движение точки В2 можно рассматривать как сложное движение, представленное переносным движением ползуна вместе с кулисой 3 и относительным движением ползуна вдоль оси кулисы. Для этого сложного движение по теореме о сложениискоростей имеем:
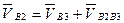 .
.
В данном векторном уравнении искомой является скорость 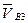 . Поэтому выполним следующее преобразование:
. Поэтому выполним следующее преобразование:
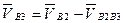 , или
, или 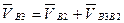 . (3.2)
. (3.2)
В последнем векторном уравнении известными являются следующие величины: модуль и направление вектора 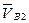 ; направление вектора
; направление вектора 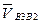 ( этот вектор противоположен вектору
( этот вектор противоположен вектору 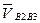 , который направлен вдоль оси кулисы 3) ; направление вектора
, который направлен вдоль оси кулисы 3) ; направление вектора 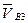 (
( 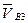
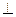 ВС). В результате имеем две неизвестные величины — модули векторов
ВС). В результате имеем две неизвестные величины — модули векторов 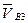 и
и 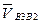 , которые могут быть определены графическим способом решения уравнения (3.2) — построением плана скоростей.
, которые могут быть определены графическим способом решения уравнения (3.2) — построением плана скоростей.
Отмечаем на плоскости произвольную точку 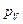 (см. рис. 3.5, б) и строим вектор
(см. рис. 3.5, б) и строим вектор 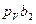 , изображающий в принятом масштабе скорость точки В2(имеем при этом в виду, что
, изображающий в принятом масштабе скорость точки В2(имеем при этом в виду, что 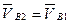 ; скорость
; скорость 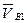 находим по заданной угловой скорости вращения кривошипа — см. выше). Далее, согласно уравнению (3.2), через конечную точку этого вектора строим прямую — направление вектора
находим по заданной угловой скорости вращения кривошипа — см. выше). Далее, согласно уравнению (3.2), через конечную точку этого вектора строим прямую — направление вектора 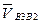 (
( 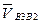
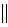 ВС), а через полюс
ВС), а через полюс 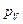 проводим прямую — направление вектора
проводим прямую — направление вектора 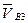 (
( 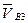
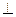 ВС). Пересечение этих направление определит точку
ВС). Пересечение этих направление определит точку 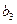 — конец вектора, изображающего на плане скоростей скорость точки В3.
— конец вектора, изображающего на плане скоростей скорость точки В3.
Численные значения скоростей 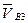 и
и 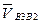 , как и выше, находим непосредственно из плана скоростей:
, как и выше, находим непосредственно из плана скоростей:
 .
.
Угловую скорость звена 3 также находим по данным плана скоростей: 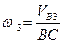 . Направление
. Направление 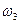 определяется направлением скорости
определяется направлением скорости 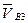 . Угловая скорость звена 2 совпадает с угловой скоростью звена 3, поскольку относительное движение этих звеньев — поступательное.
. Угловая скорость звена 2 совпадает с угловой скоростью звена 3, поскольку относительное движение этих звеньев — поступательное.
Скорость любой произвольной точки механизма, для которого построен план скоростей (построение плана скоростей можно считать завершенным, если определены векторы скорости всех кинематических пар механизма), можно найти из того же плана, используя известное из курса ТМ правило о подобии фигур кинематической схемы механизма и его плана скоростей, обозначенных одноименными символами, и выполняя соответствующие дополнительные построения.
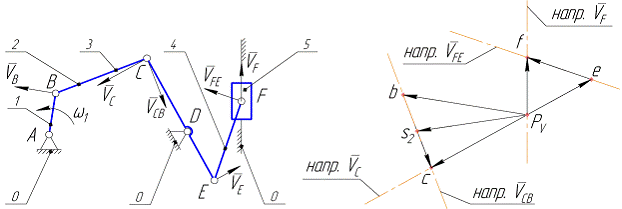
Пусть, например, построен план скоростей для механизма, включающего начальный механизм и последовательно присоединенные к нему две группы II класса (см. рис. 3.6). Необходимо найти скорость точкиЕ и скорость центра масс звена 2.
а) б)
Рис. 3.6
Вначале отметим, что неподвижным точкам механизма на его кинематической схеме соответствует полюс плана скоростей (это вполне корректное замечание, поскольку полюс можно рассматривать как вектор, начало и конец которого совпадают, т.е. как нуль-вектор скорости неподвижной точки). Это положение зафиксируем на плане скоростей, указав рядом с обозначением полюса строчные буквы, одноименные обозначениям неподвижных точек механизма, например, обозначениям кинематических пар, соединяющих подвижные звенья со стойкой (см. рис. 3.6, б).
Вектор скорости точкиЕ найдем, используя подобие фигур: отрезка СDE на кинематической схеме механизма и отрезкаc 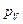 e на плане скоростей. В подобных фигурах соответствующие отрезки пропорциональны, поэтому имеем:
e на плане скоростей. В подобных фигурах соответствующие отрезки пропорциональны, поэтому имеем:
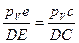
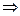
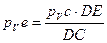
Вектор скорости центра масс звена 2 найдем из предположения, что звено 2 есть однородный стержень постоянного поперечного сечения и его центр масс расположен в геометрическом центре стержня, т.е. посередине между точкамиВ и С. Соответственно, в силу подобия, точка 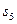 на плане скоростей будет располагаться посередине отрезка bcи скорость центра масс звена 2 изобразится вектором
на плане скоростей будет располагаться посередине отрезка bcи скорость центра масс звена 2 изобразится вектором 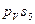 .
.
3.3.2. Построение планов ускорений
Как и выше, последовательно рассмотрим построение плана ускорений для двух типов механизмов, приведенных выше. Вначале рассмотрим кривошипно-коромысловый механизм (см. рис. 3.7, а).
При построении плана ускорений для заданного механизма предварительно определим ускорения точек входного звена по заданному закону его движения. Приэтом имеем в виду, что согласно Заданию на проект исследованию подлежат механизмы, у которых закон движения входного звена — кривошипа — представлен постоянной угловой скоростью его вращения.
Вычислим ускорение концевой точки кривошипа — кинематической пары В. Точка совершает криволинейное движение по определенной траектории — окружности радиусом АВ, т.е. можно использовать метод определения кинематических характеристик точки при естественном способе задания её движения.
Ускорение точкиВ, согласно указанному методу, можно представить двумя составляющими: нормальной и касательной:
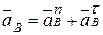 .
.
В силу постоянства угловой скорости вращения кривошипа второе слагаемое в правой части данного уравнения есть нуль-вектор. Поэтому имеем: ускорение точкиВ есть вектор, направленный вдоль оси кривошипа от точки В к точке А и равный по модулю 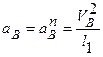 .
.
Далее определим ускорение точки С. При этом будем исходить из соотношения между ускорениями двух точек твердого тела, полученного в курсе ТМ. Принимаем точкуВ за полюс и получаем:
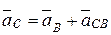 .
.
ТочкаС в её относительном движении вокруг точки В движется по окружной траектории, поэтому выполняем разложение вектора 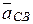 на нормальную и касательную составляющие:
на нормальную и касательную составляющие:
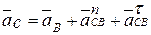 (3.3)
(3.3)
Модуль нормальной составляющей определим расчетным путем: 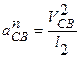 .
.
Далее устанавливаем, что в векторном уравнении (3.3) содержатся четыре неизвестные: модуль и направление вектора 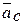 , а также модули векторов
, а также модули векторов 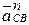 и
и 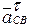 . (направления этих двух векторов известны из курса ТМ - первый вектор направлен
. (направления этих двух векторов известны из курса ТМ - первый вектор направлен
из точки С в точку В, второй - перпендикулярном направлении). Поэтому делаем вывод :уравнение (3.3) не имеет единственного решения.
Дополнительное уравнение получаем, обращаясь к соотношению между ускорениями точекС и D звена 3. Аналогично предыдущему имеем:
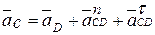 (3.4);
(3.4);
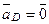 ;
; 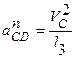 .
.
Объединяем векторные уравнения (3.3), (3.4) в одно уравнение, в котором остаются только две неизвестные — модули касательных ускорений:
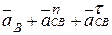
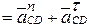 .
.
Решаем это уравнение графическим методом — строим по этому уравнению план ускорений.
Выбираем на плоскости произвольную точку 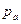 — полюс плана ускорений (см. рис. 3.7, б) и выполняем построение левой части уравнения в следующей последовательности. Из полюса
— полюс плана ускорений (см. рис. 3.7, б) и выполняем построение левой части уравнения в следующей последовательности. Из полюса 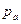 в принятом масштабе
в принятом масштабе 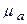
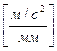 откладываем вектор
откладываем вектор 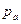 b, изображающий ускорение точки b(
b, изображающий ускорение точки b( 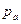 b
b 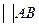 ). Из конца этого вектора строимвектор
). Из конца этого вектора строимвектор 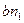 , изображающий нормальное ускорение
, изображающий нормальное ускорение 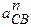 (
( 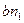
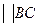 и направлен отС к В). Через конечную точку вектора проводим направление касательного ускорения
и направлен отС к В). Через конечную точку вектора проводим направление касательного ускорения 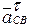 перпендикулярно оси звена 2.
перпендикулярно оси звена 2.
Выполняем построение правой части уравнения и из полюса 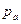 откладываем вектор
откладываем вектор 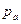
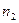 , изображающий нормальное ускорение
, изображающий нормальное ускорение 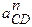 (
( 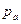
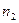
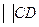 и направлен от точки C к точке D). Через конец вектора проводим направление касательного ускорения
и направлен от точки C к точке D). Через конец вектора проводим направление касательного ускорения 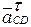 перпендикулярно оси звена 3 (см. рис. 3.7, б).
перпендикулярно оси звена 3 (см. рис. 3.7, б).
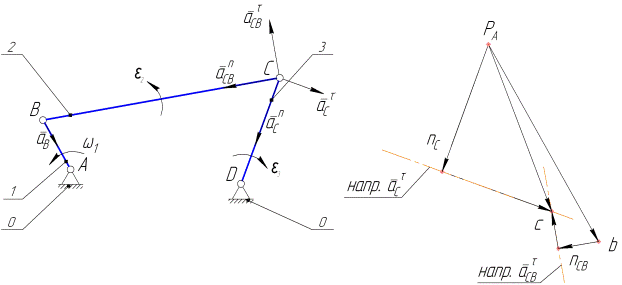
а) б)
Рис. 3.7
В пересечении направлений касательных ускорений получаем точку с конец вектора 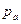 с, изображающего на плане ускорений ускорение точки С. Отмечаем, что полученный векторный многоугольник полностью отвечает приведенным выше векторным уравнениям (3.3) и (3.4).
с, изображающего на плане ускорений ускорение точки С. Отмечаем, что полученный векторный многоугольник полностью отвечает приведенным выше векторным уравнениям (3.3) и (3.4).
Построение плана ускорений завершено и непосредственно из плана находим модули неизвестных ускорений:
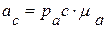 ;
; 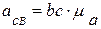 ;
; 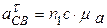
Также находим угловые ускорения звеньев 2, 3: 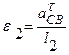 ;
; 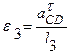
Направления этих угловых ускорений определяются направлениями соответствующих касательных ускорений (см. рис. 3.7а). Рассмотрим далее построение плана ускорений для кривошипно-кулисного механизма (см. рис. 3.8, а) и отметим некоторые особенности этой операции.
Как и выше, полагаем, что кривошип 1 вращается с постоянной скоростью, соответственно ускорение точкиВ будет иметь только нормальную составляющую, по модулю равную: 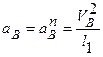 .
.
Далее отмечаем, что точку В можно отнести к трем звеньям, поэтому в дальнейшем будем рассматривать точку 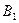 кривошипа 1, точку
кривошипа 1, точку 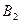 ползуна 2 и точку
ползуна 2 и точку 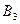 кулисы 3. Все эти точки в рассматриваемом положении механизма геометрически совпадают, однако, если точки
кулисы 3. Все эти точки в рассматриваемом положении механизма геометрически совпадают, однако, если точки 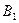 и
и 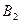 неподвижны друг относительно друга и имеют, соответственно, одинаковые кинематические характеристики, то точка
неподвижны друг относительно друга и имеют, соответственно, одинаковые кинематические характеристики, то точка 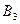 кулисы перемещается относительно точки
кулисы перемещается относительно точки 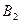 ползуна и это относительное движение — поступательное вдоль оси звена 3. В результате сначала отметим, что имеет место равенство:
ползуна и это относительное движение — поступательное вдоль оси звена 3. В результате сначала отметим, что имеет место равенство: 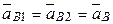 , затем перейдем к определению ускорения точки
, затем перейдем к определению ускорения точки 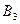 .
.
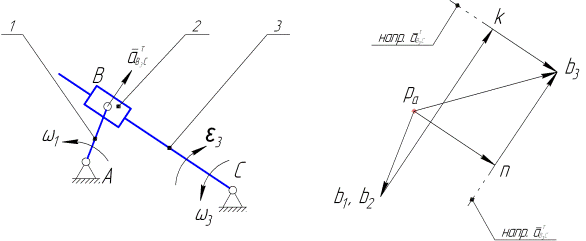
а) б)
Рис.3.8
Как и выше, будем использовать уравнения, связывающие ускорение точки 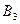 с известными ускорениями других точек механизма. Сначала обратимся к уравнению, связывающему ускорения точек
с известными ускорениями других точек механизма. Сначала обратимся к уравнению, связывающему ускорения точек 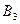 и
и 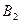 . Исходим из того, что если рассматривать в некоторой совокупности движение точек ползуна 2 и кулисы 3, то устанавливаем, что точка
. Исходим из того, что если рассматривать в некоторой совокупности движение точек ползуна 2 и кулисы 3, то устанавливаем, что точка 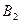 ползуна совершает сложное движение, при этом переносным её движением является движение точки
ползуна совершает сложное движение, при этом переносным её движением является движение точки 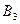 , геометрически совпадающей с точкой
, геометрически совпадающей с точкой 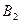 , а относительным движением является поступательное движение точки
, а относительным движением является поступательное движение точки 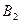 вдоль оси звена 3 относительно точек этого звена, в том числе и относительно точки
вдоль оси звена 3 относительно точек этого звена, в том числе и относительно точки 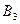 . При таком сложном движении точки, в котором переносным является вращательное движение, абсолютное ускорение точки определяется по теореме Кориолиса. Согласно этой теореме имеем:
. При таком сложном движении точки, в котором переносным является вращательное движение, абсолютное ускорение точки определяется по теореме Кориолиса. Согласно этой теореме имеем:
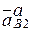 =
= 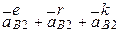 ,
,
где 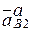 — абсолютное ускорение точки
— абсолютное ускорение точки 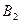 (ускорение в неподвижной системе координат);
(ускорение в неподвижной системе координат); 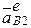 — переносное ускорение точки
— переносное ускорение точки 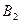 (ускорение точки, принадлежащей звену 3 и геометрически совпадающей в рассматриваемом положении с точкой
(ускорение точки, принадлежащей звену 3 и геометрически совпадающей в рассматриваемом положении с точкой 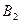 ). Этой точкой, как указывалось выше, является точка
). Этой точкой, как указывалось выше, является точка 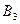 , поэтому имеем:
, поэтому имеем: 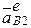 =
= 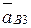 ;
; 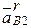 —относительное ускорение точки
—относительное ускорение точки 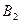 (ускорение этой точки в её движении относительно точек кулисы, в том числе относительно точки
(ускорение этой точки в её движении относительно точек кулисы, в том числе относительно точки 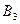 , т.е.
, т.е. 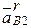 =
= 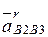 ; здесь и далее в нижней индексации первой будем указывать точку, движение которой относительно точки, стоящей второй в индексации, актуально в данном рассмотрении; смысл такой индексации следует из дальнейшего);
; здесь и далее в нижней индексации первой будем указывать точку, движение которой относительно точки, стоящей второй в индексации, актуально в данном рассмотрении; смысл такой индексации следует из дальнейшего); 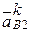 — кориолисово ускорение, характеризующее изменение относительной скорости точки
— кориолисово ускорение, характеризующее изменение относительной скорости точки 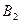 её переносном движении, определяется как удвоенное векторное произведение вектора угловой скорости переносного движения и вектора относительной скорости точки:
её переносном движении, определяется как удвоенное векторное произведение вектора угловой скорости переносного движения и вектора относительной скорости точки: 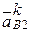 = 2 (
= 2 ( 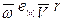 ), где
), где 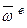 — вектор угловой скорости переносного движения, т.е.
— вектор угловой скорости переносного движения, т.е.
в нашем случае это угловая скорость кулисы 3: 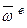 =
= 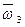 ;
; 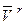 — вектор относительной скорости точки
— вектор относительной скорости точки 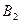 , т.е. скорость точки
, т.е. скорость точки 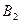 относительно точки
относительно точки 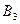 :
: 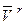 =
= 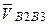 .
.
Таким образом, 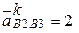 (
( 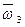 ´
´ 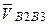 ).
).
Замечание.Здесь в обозначении кориолисова ускорения также принята индексация, упомянутая ранее и смысл которой будет ясен ниже.
Согласно определению векторного произведения модуль кориолисова ускорения равен удвоенному произведению модулей перемножаемых векторов и синуса угла между ними. Однако, поскольку в Задании на проект представлены плоские механизмы, то для всех этих механизмов векторы угловых скоростей вращающихся звеньев направлены перпендикулярно плоскости, в которой движутся звенья механизма, поэтому указанный угол равен 90 градусов и модуль кориолисова ускорения будет определяться так:
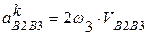
Направлено кориолисово ускорение также в соответствии с определением векторного произведения, т.е. таким образом, что векторы 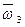 ,
, 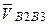 и
и 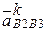 (именно в таком порядке) образуют правую тройку векторов.т.е. вектор
(именно в таком порядке) образуют правую тройку векторов.т.е. вектор 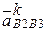 направлен перпендикулярно плоскости векторов
направлен перпендикулярно плоскости векторов 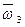 и
и 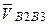 в ту сторону, откуда кратчайший поворот от вектора
в ту сторону, откуда кратчайший поворот от вектора 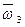 к вектору
к вектору 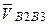 виден как вращение против часовой стрелки.
виден как вращение против часовой стрелки.
На практике для плоских механизмов удобно пользоваться правилом определения направления кориолисова ускорения, непосредственно следующим из графического представления приведенных выше положений: направление кориолисова ускорения определяется поворотом вектора относительной скорости в сторону переносного вращения на 90 градусов.
В результате выполненного анализа формулу для абсолютного ускорения точки 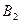 можно записать так:
можно записать так:
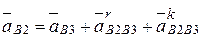 .
.
Искомым в данном векторном уравнении является ускорение точки 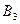 , поэтому в форме, разрешенной относительно этого ускорения, последнее уравнение принимает вид:
, поэтому в форме, разрешенной относительно этого ускорения, последнее уравнение принимает вид:
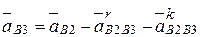 .
.
Графическое решение этого уравнения связано с построением векторов, противоположных ускорениям 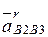 и
и 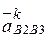 , поэтому правую часть уравнения запишем с учетом следующих формальных преобразований:
, поэтому правую часть уравнения запишем с учетом следующих формальных преобразований: 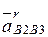 =
= 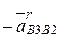 ;
; 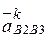 =
= 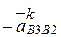 . После подстановки получаем:
. После подстановки получаем:
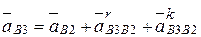 . (3.5)
. (3.5)
В данном векторном уравнении известно следующее: модуль и направление вектора 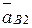 (см. выше); модуль и направление вектора
(см. выше); модуль и направление вектора 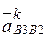 (этот вектор будет отвечать равенству
(этот вектор будет отвечать равенству 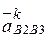 =
= 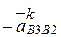 , если в формуле для определения кориолисова ускорения
, если в формуле для определения кориолисова ускорения 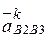 вместо вектора
вместо вектора 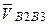 подставить вектор
подставить вектор 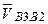 ; таким образом, слагаемое
; таким образом, слагаемое 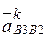 в последнем векторном уравнении будет определяться равенством
в последнем векторном уравнении будет определяться равенством 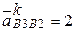 (
( 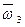 ´
´ 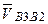 ). Соответственно модуль данноговектора будет
). Соответственно модуль данноговектора будет 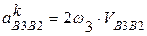 . Известн
. Известн
Дата добавления: 2021-11-16; просмотров: 504;











