Силовой расчет структурной группы II класса 2-го порядка третьего вида

Рассмотрим особенности расчета промежуточной группы Ассура, у которой центральной кинематической парой является поступательная пара V класса (рис. 4.12).

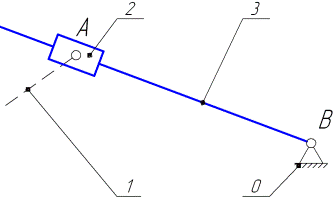
Рис. 4.12

Сначала проанализируем возможность рассмотрения равновесия звеньев по отдельности.Выделяем, например, ползун 2, прикладываем к нему активные силы и силы реакции (рис. 4.13, а) и обнаруживаем, что ползун находится под действием системы сходящихся сил и векторное уравнение равновесия этой системы содержит три неизвестные: модуль реакции 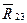,а также модуль и направление реакции 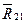. Из курса ТМ известно, что условие равновесия плоской системы сходящихся сил включает только два уравнения (в проекциях наосях координат), следовательно, в данном случае имеем статически неопределимую расчетную схему.

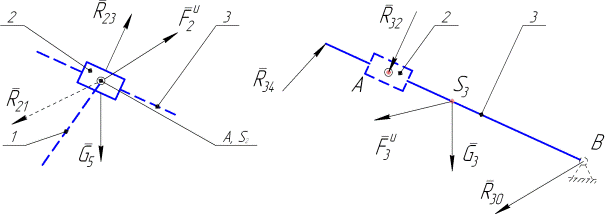
а) б)

Рис. 4.13

Выделяем далее кулису 3 (рис. 4.13, б) и получаем расчетную схему тоже с тремя неизвестными (модуль реакции 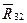, модуль и направление реакции 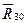). В данном случае тело (кулиса) находится под действием плоской системы сил, для исследования равновесия которой в курсе ТМ выведены три формы условия равновесия, каждая из которых включает три уравнения. Т.е. имеем статически определимую расчетную схему. Как и выше, выполним разложение реакции 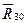на нормальную и тангенциальную составляющие (см. рис. 4.14).

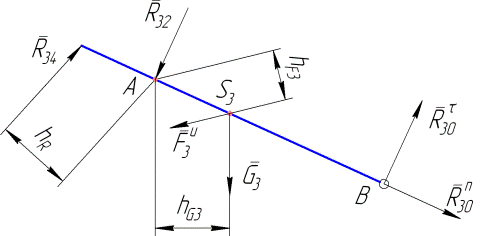
Рис. 4.14

Записываем уравнение равновесия системы сил на рисунке 4.14 в векторной форме: 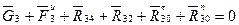(4.7)

В этом уравнении одна «лишняя» неизвестная, для отыскания которой имеет смысл обратиться к другому уравнению равновесия в форме суммы моментов сил относительно какого-либо центра. Этим центром может быть выбрана, например, точкаА, и тогда уравнение равновесия «в моментах» запишется так:

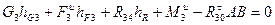(4.8)

Решаем это уравнение относительно 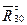и получаем модуль одной из неизвестных векторного уравнения (4.3). Модули реакци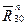й и 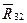найдем из плана сил, построенного по этому уравнению (см. рис. 4.15).

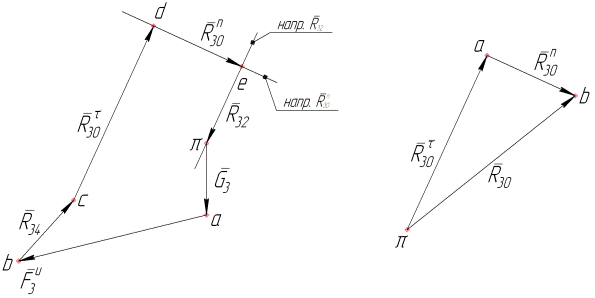
а) Рис. 4.15 б)

Более рационально, однако, при составлении уравнения равновесия «в моментах» в качестве центра выбрать точку В. Тогда решением этого уравнения будет модуль реакции 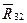и при составлении уравнения (4.3) отпадет необходимость разложения реакции 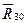на составляющие:

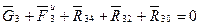(4.9)

В плане сил, построенном по этому уравнению, замыкающим вектором будет искомая реакция 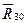(см. рис. 4.16).

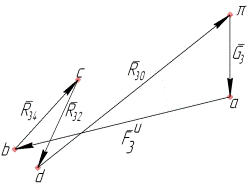
Рис.4.16

Завершающей операцией в данном анализе является отыскание реакции 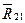, которая может быть найдена из условия равновесия ползуна 2, или группы 2-3 в целом. Проще эта задача решается, очевидно, первым способом.

Ползун находится под действием плоской системы сходящихся сил, соответственно условие его равновесия исчерпывается одним уравнением в векторной форме, или двумя алгебраическими уравнениями в координатной форме. Как и ранее, обращаемся к векторному уравнению 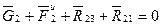и ищем его графическое решение (см. рис. 4.17).

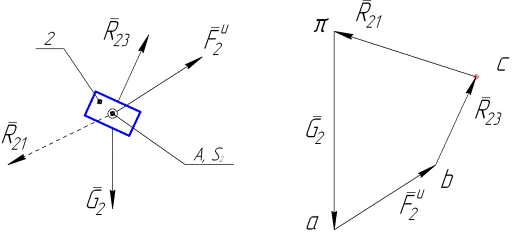
а) б)

Рис. 4.17