Силовой расчет структурной группы II класса 2-го порядка второго вида

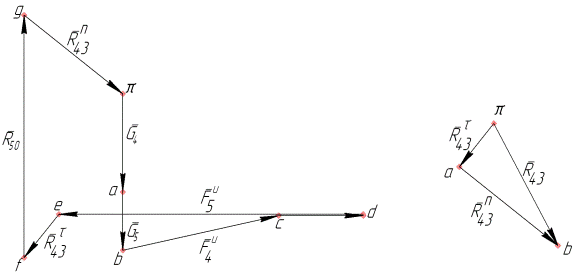
На рис. 4.1 показана группа Ассура, образованная шатуном 4, ползуном 5 и тремя кинематическими парами V класса, из которых две пары вращательные и однапара — поступательная. Шатун 4 вращательной паройА соединяется со звеном 3 промежуточной группы звеньев и вращательной парой В — с ползуном 5; ползун 5 поступательной парой В соединяется со стойкой 0 (размерами ползуна пренебрегаем, поэтому две последние кинематические пары геометрически совпадают и имеют общее обозначение символом В). Предварительно определены силы веса, главные векторы сил инерции обоих звеньев (в дальнейшем просто силы инерции) и главный момент сил инерции шатуна (в дальнейшем просто момент сил инерции). Известна также сила производственного сопротивления, приложенная к ползуну (см. рис. 4.1).

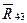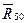Действие на звенья группы звена 3, принадлежащего предыдущей в порядке построения механизма структурной группе, и стойки 0заменяем силами и — реакциями в концевых кинематических парах группыА и В (см. рис. 4.1).

Рассматриваем равновесие группы в целом и обращаемся к системе уравнений равновесия плоской произвольной системы сил:

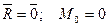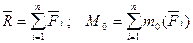, где (4.1)

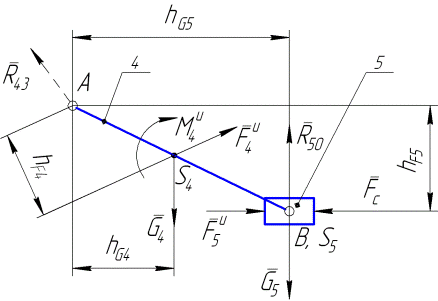
Рис. 4.1

Записываем первое из этих уравнений в развернутомвиде:

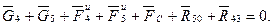(4.2)

В этом векторном уравнении три неизвестные: модули векторов и , а также направление вектора 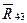. Направление вектора 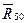известно (см. выше); точкой приложения этой реакции является точка Bв силу того, что все остальные силы, приложенные к ползуну, образуют систему сходящихся сил, так как размерами ползуна мы решили пренебречь (см. «теорему о трех силах» в курсе ТМ).

Графическое решение векторного уравнения (4.2) позволяет найти только две неизвестные, поэтому необходимо обратиться ко второму уравнению системы (4.1), при этом в целях минимизации неизвестных в этом уравнении моментной точкой выберем точку А. В развернутом виде имеем:

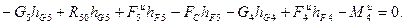
Отсюдаполучаеммодульреакции :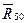

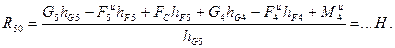
Теперь в векторном уравнении (4.2) остаются две неизвестные (модуль и направление реакции ), которые находим графическим способом, выполняя построение плана сил по этому уравнению (см. рис.4.2; неизвестная реакция на плане обозначена штриховым вектором). Построение плана сил осуществляем в следующем порядке.

Отмечаем на плоскости произвольную точку — полюс плана сил и из этой точки как из начала в принятом масштабе последовательно строим известные векторыуравнения (4.2) — от вектора 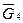до вектора 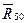, начало каждого последующего вектора присоединяя к концу предыдущего (согласно известному из курса Аналитической геометрии «правилу треугольников» сложения векторов). Последовательность построения известных векторов может быть произвольной, однако удобнее строить векторы в соответствии с записанным уравнением —уравнением (4.2).

Равенство нуль-вектору суммы нескольких векторов означает, что план сил, соответствующий этой сумме, должен быть замкнутым, т.е. конец последнего вектора в ряде слагаемых векторов должен совпадать с началом первого. Отсюда получаем: неизвестный в уравнении (4.2) вектор 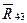находим, выполняя построение вектора, началом которого является конец вектора, изображающего на плане реакцию 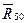(точка f), а концом — полюс плана сил 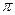(см. рис. 4.2).

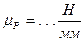
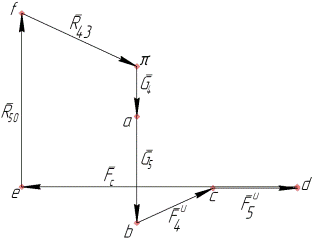
Рис. 4.2

Непосредственно из плана получаем направление искомой реакции и вычисляем её модуль: 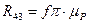, где 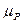— масштаб построения плана сил ( = . . . ).

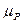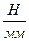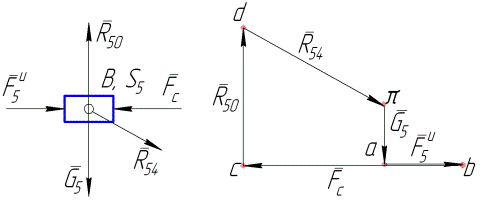
Реакцию в центральной кинематической паре рассматриваемой группы звеньев находим, исследуя равновесиекакого-либо из звеньев группы отдельно. Выделяем, например, из группы звено 5 (см. рис.4.3, а), прикладываем к нему все действующие на это звено силы, в том числе найденную реакцию 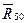и неизвестную реакцию 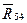, и записываем уравнение равновесия звена в форме векторной суммы всех сил:

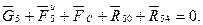
В данном уравнении также две неизвестные — модуль и направление реакции 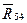, которые находим из его графического решения, выполняя по этому векторному уравнению построение плана сил (рис. 4.3, б). Направление искомой реакции следует непосредственно из плана, а модуль вычисляем с использованием масштаба плана: .

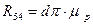На этом силовой анализ группы завершен, можно переходить к следующей (в направлении входного звена) структурной группе.

а) б)

Рис.4.3

Сделаем здесь, однако, некоторое отступление и рассмотрим другой важный частный случай группы рассматриваемого вида, когда ползун 5 имеет форму стержня и, соответственно, система сил, действующих наползун, может не являться системой сходящихся сил (рис. 4.4).

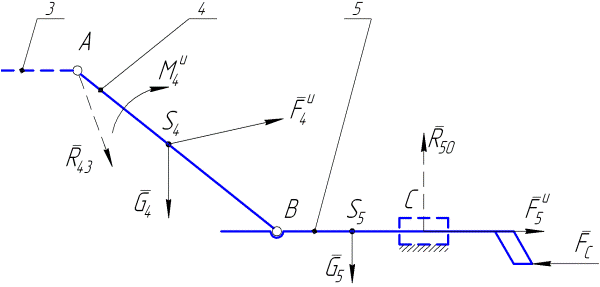
Рис.4.4

Как и выше, рассматриваем векторное уравнение равновесия группы:

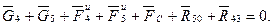(4.3)

В уравнении (4.3) также три неизвестные: модуль и направление реакции 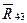, а также модуль реакции 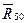(направлена эта реакция так же, как в предыдущем случае —перпендикулярно направляющей ползуна), поэтому опять необходимо обращаться к дополнительному уравнению — уравнению моментов сил. Такое уравнение актуально, когда известны направления и точки приложения искомых реакций. Вместе с тем, как указано выше, направление реакции 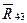заранее не определено, неизвестна также точка приложения 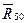. Точку приложения найдем ниже, а неопределенность направления реакции 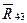устраним разложением последней на две составляющие: нормальную составляющую 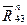, которую направим вдоль оси звена 4, и тангенциальную (касательную) составляющую 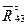, которую направим перпендикулярно оси звена. Отметим, что такое преобразование не меняет число неизвестных в уравнении (4.3). В результате появляется возможность вычисления модуля составляющей 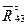, используя уравнение моментов сил, приложенных к звену 4, относительно точкиВ— центральной кинематической пары группы 4–5.

Выделяем звено 4, прикладываем все действующие на звено силы, включая и составляющие реакции 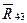, и получаем (см. рис. 4.5):

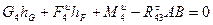. Отсюда 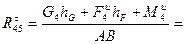. . . Н.

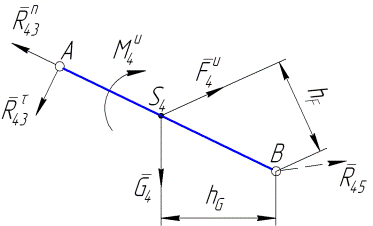
Рис. 4.5

Теперь снова обращаемся к уравнению (4.3) и обнаруживаем: с учетом разложения реакции 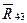на составляющие и только что вычисленного модуля 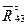данное уравнение имеет единственное решение, так как неизвестными остаются лишь модуль составляющей 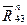и модуль реакции 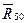(подчеркнем, что векторное уравнение инвариантно по отношению к точкам приложения слагаемых сил):

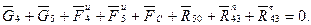
Решаем уравнение графическим методом — строим по нему план сил, замыкающими векторами которого будут искомые реакци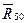и и 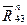(см. рис. 4.6, а).

а) б)

Рис. 4.6

Полную реакцию в кинематической пареА находим элементарным суммированием ее составляющих: 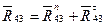(см. рис.4.6, б).

Положение точки K приложения реакции 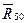определим, рассматривая условие равновесие звена 5 в форме уравнения моментов сил, действующих на звено, относительно центра B (см. рис. 4.7):

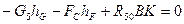
Решая это уравнение относительно плеча ВК реакции 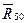, найдем искомое положение.

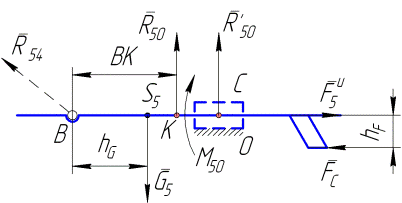
Рис. 4.7

Если задано положение поступательной пары С, реализующей подвижную связь ползуна 5 со стойкой 0 (в курсе Теоретической механики такая связь называ-

етсяскользящей заделкой), то, приводя реакцию 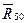к центру С, получим пару силовых факторов, характеризующих реакцию в этой паре: силу 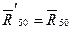момент

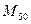(см. рис. 4.7).

Реакцию 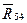( 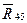) в центральной паре B рассматриваемой группы определим аналогично предыдущему из условия равновесия одного из звеньев группы.