Кинематический анализ методом диаграмм
Метод диаграмм также является графическим методом кинематического исследования механизмов, основанным на следующих относительно несложных теоретических предпосылках.
Запишем дифференциальные соотношения для угловой скорости и углового ускорения некоторого k-тогo звена механизма и выполним их тождественные преобразования.
Имеем: 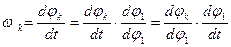 .
.
Здесь: 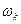 — угловая скорость k-тогo звена, рад/с;
— угловая скорость k-тогo звена, рад/с; 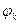 — угол поворота k-тогo звена, рад;
— угол поворота k-тогo звена, рад; 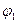 — угол поворота входного звена механизма, закон движения которого известен (условно этим звеном полагаем звено 1).
— угол поворота входного звена механизма, закон движения которого известен (условно этим звеном полагаем звено 1).
После такого преобразования имеем произведение двух множителей, второй из которых есть угловая скорость входного звена, а первый является безразмерной величиной, которую можно охарактеризовать как скорость изменения угла поворота k-тогo звена при изменении угла поворота входного звена. Называется эта величина аналогом угловой скорости k-тогo звена (обозначается символом 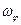 ) и, таким образом, действительная угловая скорость
) и, таким образом, действительная угловая скорость 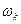 равна произведению аналога угловой скорости и действительной угловой скорости входного звена:
равна произведению аналога угловой скорости и действительной угловой скорости входного звена:
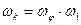 (1).
(1).
Далее: 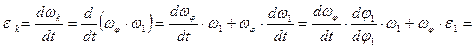
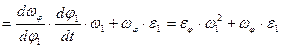 .
.
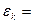
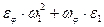 (2).
(2).
Здесь: 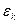 — угловое ускорение k-тогo звена, рад/с2;
— угловое ускорение k-тогo звена, рад/с2; 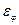 —аналог углового ускорения k-тогo звена, рад/рад2 .
—аналог углового ускорения k-тогo звена, рад/рад2 .
Аналогичным образом могут быть получены формулы, связывающие действительные скорость и ускорение какой-либо точки механизма с кинематическими параметрамивходного звена посредством аналогов скорости и ускорения данной точки:
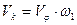 (3);
(3);
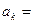
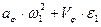 (4).
(4).
Таким образом, действительные угловая скорость и угловое ускорение произвольного звена механизма, или действительные скорость и ускорение любой его точки могут быть выражены линейными соотношениями между этими величинами и угловой скоростью и угловым ускорением того звена механизма, закон движения которого задан. Коэффициентами в этих соотношениях являются аналоги искомых скоростей и ускорений звеньев или точек механизма, в результате чего кинематическое исследование механизма может быть сведено к отысканию этих аналогов с последующим использованием формул (1) – (4).
Замечание.Соотношения, аналогичные формулам (1) – (4), можно получить и при поступательном движении входного звена механизма. Рассмотренный случай более актуален, поскольку обычно в качестве входного выбирается звено, совершающее простое вращательное движение, поскольку с таким звеном легко сопрягаются наиболее распространенные приводы, включающие электродвигатель и механизм передачи.
Как показано выше, аналоги не зависят от времени, а зависят от угла поворота входного звена. Поэтому операция отыскания аналогов может быть сведена к ряду геометрических построений, содержание которых удобнее проиллюстрировать на примере.
Пусть задан кривошипно-ползунный механизм (рис. 3.9).
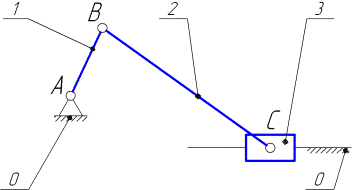
Рис. 3.9
Определим аналоги скорости и ускорения выходного звена механизма — ползуна 3 — за цикл движения, соответствующий одному обороту входного звена — кривошипа 1 — при постоянной скорости вращения входного звена (такое движение еще называется основным или перманентным).
Выше показано, что аналоги скорости и ускорения определяются на основе зависимостей, связывающих перемещение звена или точки, кинематические параметры которых являются искомыми, с перемещением входного звена (с обобщенной координатой). Поэтому вновь обращаемся к построению ряда положений механизма, достаточно близко отстоящих друг от друга для обеспечения требуемой точности результатов.
Согласно методике, приведенной в разделе 3.2, определяем крайние положения механизма (см. рис. 3.10), одно из крайних принимаем за начальное (нулевое) положение, выбираем направление вращения кривошипа и строим, например, шесть положений механизма через каждые 60 градусов поворота кривошипа (рис. 3.10). Точность результатов при таком выборе числа положений механизма будет минимальна, однако здесь приоритетом будем полагать наглядность графического материала, которая невозможна при большой плотности последнего.
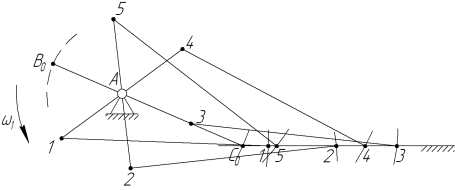
Рис. 3.10
Непосредственно из чертежа определяем значения перемещения выходного звена через каждые 60 градусов поворота кривошипа и составляем табличную функцию 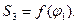
Таблица 3.1
| № пол. | |||||||
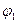 .град. .град.
| |||||||
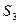 , мм , мм
| 6,8 | 24,8 | 40,9 | 32,5 |
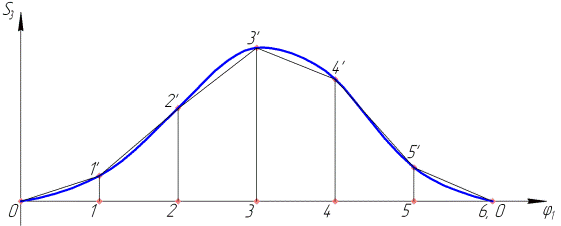
По данным таблицы строим диаграмму перемещений ползуна 3 (т.е. переводим табличную форму функции 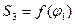 в графическую, см. рис. 3.11, а).
в графическую, см. рис. 3.11, а).
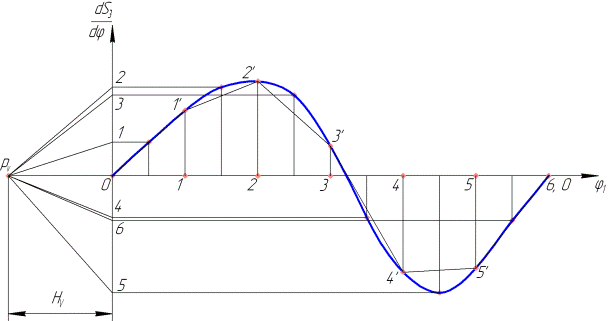
Выполняя графическое дифференцирование диаграммы перемещений, строим диаграммы аналогов скоростей и ускорений ползуна (рис. 3.11, б,в). Рассмотрим подробнее эту операцию. Исходим из геометрического смысла производной, согласно которому производная функции в некоторой точке численно равна угловому коэффициенту касательной к графику функции в этой точке.
Выполняем приближенную оценку производной на каждом частичном отрезке области определения функции 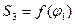 , для чего строим касательную к каждой частичной дуге кривой функции в средней точке этой дуги. Точно выполнить эту геометрическую операцию при небольших размерах частичных дуг технически сложно, поэтому обычно построение касательных заменяется построением хорд, стягивающих концевые точки частичных дуг, в предположении (достаточно обоснованном при малых размерах частичных дуг), что касательная к дуге в средней ее точке практически параллельна хорде дуги (см. рис. 3.11, а).
, для чего строим касательную к каждой частичной дуге кривой функции в средней точке этой дуги. Точно выполнить эту геометрическую операцию при небольших размерах частичных дуг технически сложно, поэтому обычно построение касательных заменяется построением хорд, стягивающих концевые точки частичных дуг, в предположении (достаточно обоснованном при малых размерах частичных дуг), что касательная к дуге в средней ее точке практически параллельна хорде дуги (см. рис. 3.11, а).
Далее вводим в рассмотрение систему координат ( 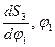 ), располагая ось ординат на продолжении оси ординат диаграммы перемещений, аось абсцисс - параллельно оси абсцисс той же диаграммы перемещений (см. рис. 3.11б)
), располагая ось ординат на продолжении оси ординат диаграммы перемещений, аось абсцисс - параллельно оси абсцисс той же диаграммы перемещений (см. рис. 3.11б)
Диаграмма перемещений звена 3
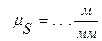
а) 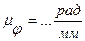
Диаграмма аналогов скоростей звена 3
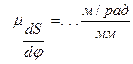
б) 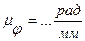
Диаграмма аналогов ускорений звена 3
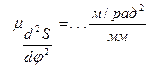
в) 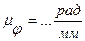
Рис. 3.11
Далее в координатах ( 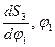 ) выполняем следующее. На продолжении оси абсцисс выбираем произвольную точку
) выполняем следующее. На продолжении оси абсцисс выбираем произвольную точку 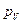 — полюс метода графического дифференцирования, из которого проводим семейство лучей, параллельных хордам на диаграмме перемещений, до пересечения этих лучей с осью ординат (см. рис. 3.11, б). Далее через точки пересечений (точки 1, 2, 3…) проводим ряд параллельных оси абсцисс прямых, а через середины частичных отрезков оси абсцисс (во всех диаграммах отрезки оси абсцисс по длине совпадают) проводим ряд вертикальных прямых. На каждом частичном отрезке отмечаем точки пересечения пар горизонтальной и вертикальной прямых, соответствующих этим отрезкам. Получаем множество точек
— полюс метода графического дифференцирования, из которого проводим семейство лучей, параллельных хордам на диаграмме перемещений, до пересечения этих лучей с осью ординат (см. рис. 3.11, б). Далее через точки пересечений (точки 1, 2, 3…) проводим ряд параллельных оси абсцисс прямых, а через середины частичных отрезков оси абсцисс (во всех диаграммах отрезки оси абсцисс по длине совпадают) проводим ряд вертикальных прямых. На каждом частичном отрезке отмечаем точки пересечения пар горизонтальной и вертикальной прямых, соответствующих этим отрезкам. Получаем множество точек  , расстояние от которых до оси абсцисс пропорционально среднему значению производной на соответствующих частичных отрезках. Обводим эти точки плавной кривой и получаем искомую диаграмму аналогов скоростей ползуна 3 за цикл движения механизма — один оборот входного звена (кривошипа 1). При построении диаграммы учитываем, что в начальном положении механизма скорость ползуна равна нулю, соответственно дополняем кривую диаграммы участками
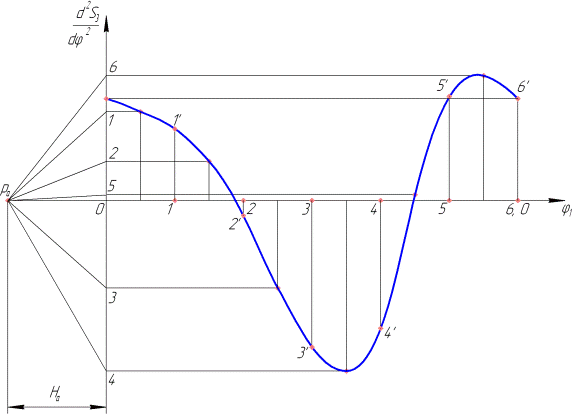
, расстояние от которых до оси абсцисс пропорционально среднему значению производной на соответствующих частичных отрезках. Обводим эти точки плавной кривой и получаем искомую диаграмму аналогов скоростей ползуна 3 за цикл движения механизма — один оборот входного звена (кривошипа 1). При построении диаграммы учитываем, что в начальном положении механизма скорость ползуна равна нулю, соответственно дополняем кривую диаграммы участками 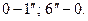 Выполняя аналогичные построения, графическим дифференцированием диаграммы аналогов скоростей получаем диаграмму аналогов ускорений звена 3 (см. рис. 3.11в). Масштабы диаграмм аналогов скоростей и ускорений определяем по формулам:
Выполняя аналогичные построения, графическим дифференцированием диаграммы аналогов скоростей получаем диаграмму аналогов ускорений звена 3 (см. рис. 3.11в). Масштабы диаграмм аналогов скоростей и ускорений определяем по формулам:
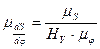 ;
; 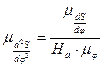 ,
,
где 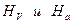 — полюсные расстояния диаграмм аналогов скоростей и аналогов ускорений соответственно, мм.
— полюсные расстояния диаграмм аналогов скоростей и аналогов ускорений соответственно, мм.
Аналогичным образом можно построить кинематические диаграммы для остальных звеньев механизма (собственно в рассмотренном примере к ним относится лишь шатун 2).
Сравнительный анализ результатов кинематического анализа методом планов и методом диаграмм выполним, разместив на одном и том же координатном поле действительные значения скорости и ускорения какой-либо точки (или действительные угловые скорости какого-либо звена), рассчитанные этими двумя методами для всех положений механизма, в которых определялись указанные кинематические параметры, и оценив разности значений. Подробнее эта операция рассмотрена в прилагаемых примерах выполнения проекта.
4. СИЛОВОЙ АНАЛИЗ РЫЧАЖНОГО МЕХАНИЗМА
Дата добавления: 2021-11-16; просмотров: 492;











