ОБРАБОТКА РЕЗУЛЬТАТОВ ЭКСПЕРИМЕНТА МЕТОДОМ ДИСПЕРСИОННОГО АНАЛИЗА

Основные понятия дисперсионного анализа

При обработке результатов активных экспериментов исследователь часто сталкивается со случаями, когда в качестве входных исследуемых факторов системы 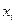выступают качественные факторы.

При этом применение регрессионного анализа невозможно, так как он оперирует величинами, измеряемыми только в количественных шкалах. В рассматриваемых условиях для оценки влияния входных факторов и их взаимодействий на выходной параметр системы Y применяется дисперсионный анализ (ДА).

Следует подчеркнуть, что в отличие от регрессионного анализа в ДА оценивается лишь влияние фактора в целом (влияет или нет) и не выясняются количественные соотношения.

Суть метода состоит в выделении и оценке отдельных факторов, вызывающих изменчивость (вариацию) выходного параметра 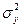на составляющие, обусловленные независимыми входными факторами, их взаимодействиями и неучтенными случайными причинами. Например, для двухфакторного ДА получим разложение вида:

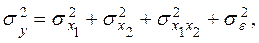(4.1)

где 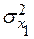– доля дисперсии, вызванная влиянием фактора x₁;

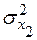– доля дисперсии, вызванная влиянием фактора x₂;

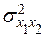– доля дисперсии, вызванная влиянием фактора x₁ и x₂;

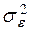– доля дисперсии, вызванная неучтенными случайными величинами.

Статистический анализ данных составляющих позволяет делать выводы о том, действительно ли оказывает влияние на выходной параметр системы тот или иной фактор, то или иное взаимодействие факторов.

Таким образом, изучение переменных факторов по их дисперсиям и называется дисперсионным анализом.

Основоположником ДА является английский статистик Р.Фишер, который в двадцатых годах нашего столетия применил для решения агробиологических задач. В настоящее время данный метод находит очень широкое применение для обработки наблюдений в самых различных областях.

Он охватывает большое число хорошо разработанных приемов планирования и обработки экспериментов, основные понятия которых будут рассмотрены в данном разделе учебного пособия.

В зависимости от числа исследуемых факторов ДА различают однофакторный и многофакторный. Факторы, рассматриваемые в ДА, могут быть двух родов:

1 со случайными уровнями.

2 с фиксированными уровнями.

В первом случае предполагается, что выбор уровней производится из бесконечной совокупности возможных уровней и сопровождается рандомизацией. При этом результаты эксперимента имеют большое значение, поскольку выводы по эксперименту можно распространить на всю генеральную совокупность. Если все уровни факторов выбираются случайными, то математическая модель эксперимента называется случайной моделью (моделью со случайными уровнями факторов). Когда все уровни фиксированы, модель называется моделью с фиксированными уровнями факторов. Когда часть факторов рассматривается на фиксированных уровнях, а часть на случайных, то моделью смешанного типа.

Влияние изучаемых входных факторов x_i на выходной параметр системы Y может быть двояким. Они могут изменять как истинный результат – среднее наблюдений, так и дисперсию этих наблюдений. Мы, однако, все время будем предполагать, что дисперсия наблюдений остается неизменной. Это предположение обычно оправдывается, если в ходе эксперимента для получений наблюдений используется одна и та же методика, одни и те же приборы. Если же стабильность дисперсий вызывает сомнение, следует провести проверку их однородности по критерию Кохрена или Бартлета. В случае значимого изменения дисперсии в процессе наблюдений нужно попытаться ее стабилизировать, подобрав соответствующую преобразующую функцию. Это дает возможность рассматривать все наблюдения как выборку из одной генеральной совокупности.

Исходя из сказанного, в ДА изучается лишь влияние входных факторов x_i на генеральное среднее наблюдаемого распределения выходного параметра Y.

Таким образом, при проведении ДА предполагается, что выполняются следующие условия.

1 Результаты наблюдений выходного параметра системы Y являются независимыми случайными величинами, имеющими нормальный закон распределения.

2 Случайные ошибки наблюдений подчиняются нормальному закону распределения.

3 Входные исследуемые факторы x_i влияют только на изменение средних значений, а дисперсия наблюдений остается постоянной.

4 Эксперименты равноточны.

Проверка данных условий перед проведением ДА обязательна.

Рассмотрим наиболее простой случай однофакторного ДА, когда генеральная дисперсия наблюдений 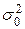известна заранее. Пусть при изменении фактора Х получились результаты наблюдений 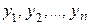, которые удовлетворяют перечисленным выше требованиям. Найдем оценку дисперсии выходного параметра Y:

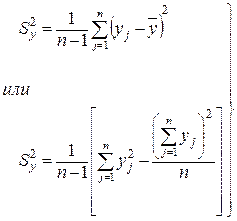. (4.2)

Сравним эту дисперсию, имеющую n - 1 степень свободы, с генеральной дисперсией наблюдени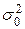й Если 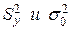отличаются незначимо, то и влияние фактора Х нужно признать незначимым, так как он не сумел существенно увеличить случайный разброс наблюдений.

Если же 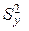отличается значимо от 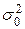, то это может быть вызвано только влиянием фактора Х, которое теперь нужно признать значимым. Для оценки дисперсии 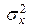воспользуемся тем, что дисперсия суммы двух независимых случайных величин равна сумме их дисперсий. В нашем случае складывается эффект случайности, имеющий дисперсию 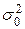, и эффект воздействия фактора Х с дисперсией 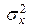, которые независимы. Поэтому общая дисперсия наблюдений будет равна:

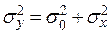. (4.3)

Оценкой данной дисперсии будет являться выборочная дисперсия 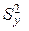, определяемая по зависимости (4.2)

Следовательно, имеем:

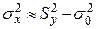. (4.4)

Сравнение дисперсий 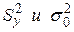осуществляется по критерию Фишера, где влияние фактора Х признается значимым, если при уровне значимости 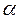и степенях свободы 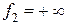знаменателя выполняется условие:

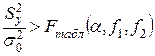. (4.5)

В противном случае влиянием фактора Х следует пренебречь.

Значение F – критерия находится по таблице приложения Б.

Расчеты по приведенной выше схеме очень просты, однако в большинстве случаев заранее величина дисперсии наблюдений 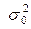нам не будет известна. Поэтому рассмотренная методика хороша лишь с методологической точки зрения.