Однофакторный дисперсионный анализ

Рассмотрим действие на выходной параметр системы Y только одного входного фактора Х, который принимает m различных значений (постоянных уровней). Так как, в общем случае генеральная дисперсия наблюдений 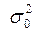нам не известна, то для вычисления оценки нужно обязательно иметь дублирующие (параллельные) наблюдения. Здесь можно поступить по-разному: можно на первом же уровне x₁, привести достаточно много наблюдений, вычислить оценку дисперсии и использовать ее для изучения других уровней. Лучше, однако, повторять наблюдения на всех уровнях, так как при этом появляется дополнительная возможность контроля за неизменностью дисперсии 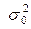. Наиболее простые расчеты получаются в случае, когда на каждом уровне фактора x_i производится одинаковое число наблюдений n₁=n₂=…=n_i=…=n_m=n. Результаты наблюдений обычно оформляют в виде следующей таблицы.

Таблица 4.1 – Исходные данные для ДА с равным числом повторений опытов

Номер опыта	Уровни фактора Х
x1	x2	…	xi	…	xm
… j … n	y11 y21 … yj1 … yn1	y12 y22 … yj2 … yn2	… … … … … …	y1i y2i … yji … yni	… … … … … …	y1m y2m … yjm … ynm
Групповые средние			…		…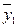

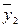
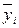
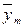
В таблице 4.1 обозначено:

j=1,n – число опытов на каждом уровне фактора х;

i=1,m – число уровней фактора х.

В последней строке таблице 4.1 записаны средние арифметические значения полученных наблюдений выходного параметра Y для каждого из уровней фактора Х:

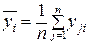, (4.6)

где у_ji – j-е значение выходного параметра у на i – м уровне.

Пусть результаты измерений выходного параметра у_ji распределены по нормальному закону, имеют одинаковую, хотя и неизвестную дисперсию:

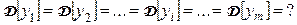
Требуется при заданном уровне значимости 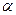по выборочным средним (оценкам математического ожидания) проверить нулевую гипотезу о равенстве всех математических ожиданий:

.

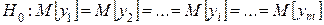Будем полагать, что для i-го уровня n наблюдений имеют среднюю 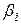, которая равна сумме общей средней 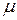и вариации ее, обусловленной i-м уровнем фактора х, то есть:

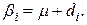(4.7)

В рассматриваемых условиях любое наблюдение из таблицы 4.1 может быть представлено в виде следующей модели:

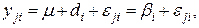(4.8)

где 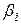– средняя для i-го уровня фактора х;

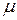– генеральное среднее результатов наблюдений или общая средняя (математическое ожидание для среднего во всей таблица 4.1);

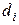– эффект фактора х на i-м уровне (отклонение математического ожидания выходного параметра при i-м уровне фактора 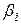от общего математического ожидания );

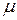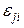– вариация результатов внутри отдельного уровня (случайный остаток, характеризующий влияние на 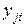всех неучтенных моделью (4.8) факторов).

Согласно общей идее ДА разложим оценку дисперсии выходного параметра 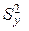на составляющие, которые характеризовали бы вклад фактора х и фактора случайности:

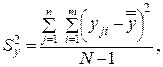(4.9)

где N – общее число опытов;

N=n₁=n₂=…=n_i=…=n_m=mn;

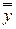– общая средняя для всей выборки;

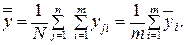
При расположении наблюдений так, как показано в таблице 4.1, их рассеяние между строками обуславливается ошибкой воспроизводимости эксперимента, а рассеяние между столбцами – дополнительным действием исследуемого фактора х. Рассеяние отдельных наблюдений относительно общего среднего 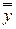обусловлено действием, как случайных причин, так и влиянием фактора х. Действие фактора случайности проявляется в рассеянии (с дисперсией 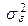) наблюдений серий параллельных опытов 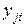на каждом уровне x_i вокруг среднего арифметического 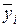своей серии. Влияние же фактора х (с дисперсией 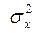) вызывает повышенное рассеяние средних арифметических 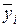серий относительно общего среднего 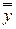. Каждое их этих трех рассеяний можно охарактеризовать соответствующей суммой квадратов отклонений.

С этой целью преобразуем общую сумму квадратов отклонений наблюдений 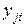от общего среднего 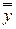(числитель (4.9)) к следующему виду:

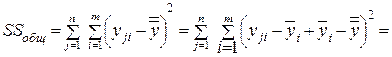
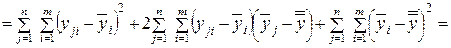(4.10)

.

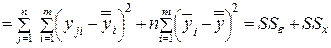Вследствие того, что:

,

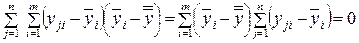поскольку:

.

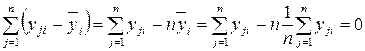Суммы 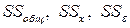, входящие в выражение (4.10), означают следующее:

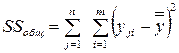; (4.11)

– это общая сумма квадратов отклонений отдельных наблюдений 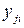от общего среднего 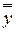. Она характеризует рассеяние наблюдений в результате действия, как фактора случайности 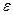, так и исследуемого входного фактора х;

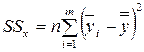; (4.12)

– это сумма квадратов отклонений между средними по уровням 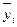и общей средней 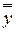. Сумма SS_x/n рассеяние средних 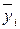уровней за счет случайных причин (с дисперсией 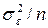для средних уровней) и исследуемого входного фактора х (с дисперсией );

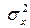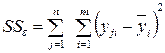; (4.13)

– это сумма квадратов отклонений внутри уровней, то есть сумма квадратов разностей между отдельными наблюдениями 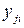и средним 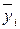соответствующего уровня. Она характеризует остаточное рассеяние случайных погрешностей опытов, то есть их воспроизводимость.

Таким образом, общую сумму квадратов отклонений наблюдаемых значений выходного параметра от общей средней 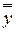мы разложили на две составляющие: 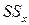– факторную сумму квадратов отклонений и 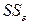– остаточную сумму квадратов отклонений.

Зная суммы квадратов 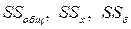, можно определить соответствующие оценки дисперсий: общую, межуровневую и внутриуровневую :

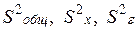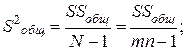(4.14)

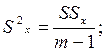(4.15)

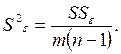(4.16)

Оценки 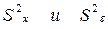в литературе достаточно часто называют факторной и остаточной дисперсиями.

Математически строго можно показать, что если влияние входного исследуемого фактора х на выходной параметр Y несущественно, то полученные нами дисперсии (4.14)-(4.16) являются несмещенными оценками генеральной дисперсии наблюдений 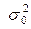, то есть:

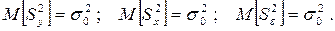(4.17)

Следовательно, для выяснения влияния фактора Х на выходной параметр Y необходимо сравнить дисперсии 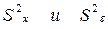. Для того, чтобы влияние фактора было признано значимым, необходимо и достаточно, чтобы оценка дисперсии 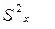значимо отличалась от 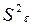. Проверку нуль-гипотезы об однородности этих оценок можно осуществить по критерию Фишера:

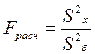. (4.18)

Если вычисленное по результатам наблюдений дисперсионное отношение F_расч превосходит критическое табличное 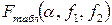, найденное по распределению Фишера для выбранного уровня значимости 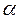и степеней свободы 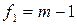числителя и 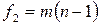знаменателя (2.18),

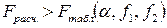, (4.19)

то влияние фактора Х следует признать значимым. Если условие (4.19) не выполняется, то есть:

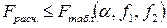, (4.20)

то влияние фактора Х следует признать незначимым. Так как в рассматриваемых условиях проверяется нулевая гипотеза:

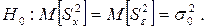
при конкурирующей гипотезе вида:

,

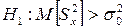то при расчетах следует пользоваться односторонним F-критерием (приложение Б).

Таким образом, если выполняется условие (4.19), то дисперсии 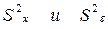значимо отличаются друг от друга, нулевая гипотеза равенства средних:

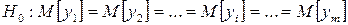
должна быть отвергнута и влияние фактора Х признано значимым. В этих условиях по результатам наблюдений (смотреть таблицу 4.1) можно оценить:

– дисперсию воспроизводимости 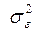- выборочной остаточной дисперсией:

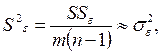
то есть:

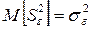(4.21)

и определить доверительный интервал для 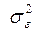по х₂-распределению с m(n-1) степенями свободы;

– дисперсию исследуемого фактора Х по формуле:

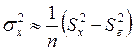, (4.22)

– расхождение 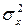генеральных центров серий, обусловленное влиянием фактора Х. Так как

,

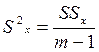то можно показать, что

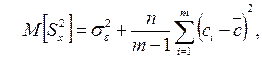
где 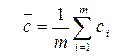– среднее значение из генеральных центров распределения с_i,

или

.

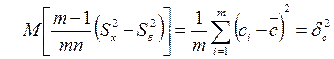Оценкой величины 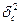служит выборочная характеристика

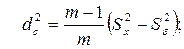(4.23)

– расхождение 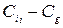между генеральными центрами любых двух серий.

Так как статистика

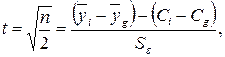(4.24)

следует распределению Стьюдента с числом степеней свободы 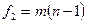, то интервал

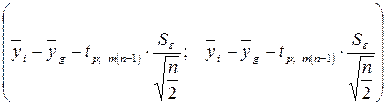(4.25)

служит доверительным (1-р)100 % интервалом для ;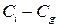

– сравнение всех средних при помощи множественного рангового критерия Дункана, попарное сравнение по t-критерию и другие.

При интерпретации результатов ДА необходимо иметь в виду, что очень низкое значение дисперсионного отношения может быть связано с тем, что влияние какого-то важного неконтролируемого в ходе эксперимента не было рандомизировано.

Это может увеличить дисперсию внутри уровней, а дисперсию между уровнями оставить неизменной, что уменьшает дисперсионное отношение. В данном случае результаты проведенных экспериментов уже не будут подчиняться модели (4.8).

При интерпретации результатов ДА для математической модели со случайными уровнями факторов обычно интересуются не проверкой гипотез относительно средних, а оценкой компонент дисперсий. В отличие от модели с фиксированными уровнями выводы по случайной модели распространяются на генеральную совокупность уровней.