Скорость и ускорение
Перемещение и путь
Для изучения закономерностей физических процессов используют физические модели. Физической моделью, используемой для изучения законов механического движения является материальная точка– тело, обладающее массой, но размерами которого можно пренебречь в условиях данной задачи.
Рассмотрим кинематику материальной точки. Существует два способа геометрического описания движения точки.
Первый способ. С помощью радиус-вектора 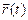 , являющегося функцией времени t, который фиксирует положение материальной точки М по отношению к некоторой точке О (начало координат – рис. 1.1).
, являющегося функцией времени t, который фиксирует положение материальной точки М по отношению к некоторой точке О (начало координат – рис. 1.1).

Рис. 1.1
Для прямоугольной (декартовой) системы координат вектор 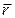 может быть представлен в виде трех независимых координат:
может быть представлен в виде трех независимых координат:
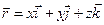 (1.1)
(1.1)
При движении материальной точки ее координаты изменяются со временем и определяются скалярными уравнениями:
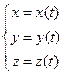 (1.2)
(1.2)
Это параметрические уравнения траектории, где параметром является время t, а 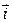 ,
, 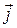 ,
, 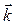 – единичные векторы соответствующих осей.
– единичные векторы соответствующих осей.
Число независимых координат, определяющих положение материальной точки в пространстве, называется числом степеней свободы.
Второй способ. С помощью траектории, по которой движется точка и уравнения ее движения по этой траектории. Траектория (или пройденный путь) – это непрерывная линия, которую описывает точка при своем движении (рис. 1.2).
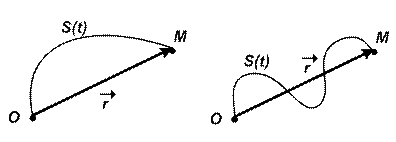
Рис. 1.2
Прямая, проведенная из точки, в которой началось движение, в точку, где находится материальная точкав определенный момент времени, называетсявектором перемещения.В общем случае векторперемещения не совпадает с траекторией, но при достаточно малом перемещениитраекторию можно заменить хордой. Длина траектории совпадает с длиной вектора перемещения и в случае прямолинейного движения.
Скорость и ускорение
Рассмотрим движение материальной точки из положения А в положение В вдоль произвольной траектории 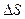 (рис. 1.3). Положения материальной точки в начальный и конечный момент времени определяются радиус-векторами
(рис. 1.3). Положения материальной точки в начальный и конечный момент времени определяются радиус-векторами  и
и 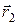 ; за время
; за время 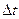 материальная точка проходит путь
материальная точка проходит путь 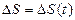 и получает приращение радиус-вектора
и получает приращение радиус-вектора 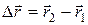 –вектор перемещения.
–вектор перемещения.
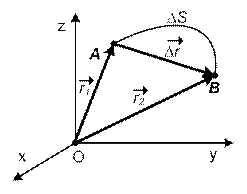
Рис. 1.3
Среднюю скорость можно определить как
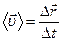 (1.3)
(1.3)
В случае малого промежутка времени ( 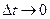 ), получаем выражение для мгновенной скорости
), получаем выражение для мгновенной скорости 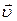
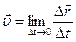 (1.4)
(1.4)
Математически понятие мгновенной скорости совпадает с определением производной (или иначе: физический смысл понятия производной есть мгновенная скорость)
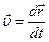 (1.5)
(1.5)
Скорость–векторная величина, направление которой определяется касательной к траектории в данной точке. Для вектора скорости справедливо векторное сложение.
 (1.6)
(1.6)
Например, такое часто наблюдается в строительстве. Так, автомобильный кран, имеющий выдвижную стрелу, поднимает груз. При этом стрела, находясь под углом, выдвигается и еще вращается вокруг вертикальной оси. Груз участвует в трех движениях и обладает, соответственно, скоростями: вверх - 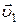 , вдоль оси стрелы -
, вдоль оси стрелы - 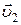 и окружной скоростью
и окружной скоростью 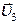 . Результирующая скорость
. Результирующая скорость 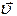 будет:
будет:
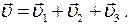
Часто на практике используется средняя скорость.
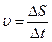 – средняя скорость (1.7)
– средняя скорость (1.7)
При достаточно малом промежутке времени 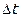 имеем
имеем 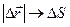
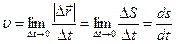 – мгновенная скорость (1.8)
– мгновенная скорость (1.8)
Физическая величина, характеризующая быстроту изменения скорости по величине и по направлению при неравномерном движении, называетсяускорением. Если за промежуток времени 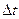 скорость изменилась на
скорость изменилась на 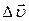 , то
, то
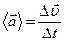 –среднее ускорение (1.9)
–среднее ускорение (1.9)
 – мгновенное ускорение (1.10)
– мгновенное ускорение (1.10)
Пусть материальная точка движется по криволинейной траектории со скоростью 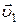 , которая изменяется по величине и по направлению (рис. 1.4). За время
, которая изменяется по величине и по направлению (рис. 1.4). За время 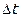 точка переместилась из положения А в положение В и прошла путь
точка переместилась из положения А в положение В и прошла путь 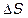 , равный дуге АВ. За это время материальная точка приобрела скорость
, равный дуге АВ. За это время материальная точка приобрела скорость 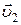 . Переместив вектор
. Переместив вектор 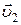 в положение А, определим приращение скорости на пути АВ; оно будет равно
в положение А, определим приращение скорости на пути АВ; оно будет равно 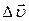 .
.
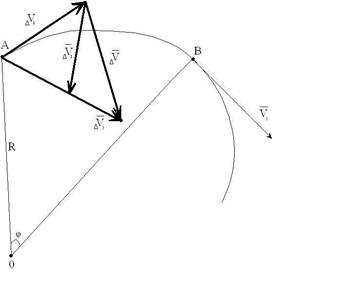
Рис. 1.4
Разложим 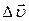 на
на  составляющие
составляющие 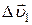
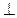
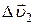 и
и 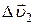 , совпадающий с
, совпадающий с 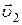 .
.
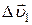 – характеризует изменение скорости по направлению;
– характеризует изменение скорости по направлению;
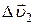 – характеризует изменение скорости по величине:
– характеризует изменение скорости по величине:
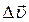 =
= 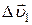 +
+ 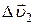 (1.11)
(1.11)
Ускорение будет равно
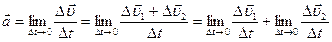 (1.12)
(1.12)
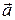 – полное ускорение, состоящее из двух компонент.
– полное ускорение, состоящее из двух компонент.
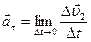 – тангенциальное (или касательное) ускорение, характеризующее изменение скорости по модулю за время
– тангенциальное (или касательное) ускорение, характеризующее изменение скорости по модулю за время 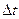 . Это означает, что тангенциальное ускорение есть производная от скорости по времени.
. Это означает, что тангенциальное ускорение есть производная от скорости по времени.
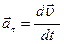 (1.13)
(1.13)
Тангенциальное ускорение 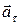 – векторная величина, направленная в сторону вектора скорости.
– векторная величина, направленная в сторону вектора скорости.
Определим составляющую 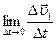 .
.
Эта составляющая характеризует изменение скорости по направлению и называется нормальным ускорением
 (1.14)
(1.14)
При 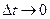 точка А близка к точке В. В этом случае путь
точка А близка к точке В. В этом случае путь 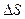 можно считать дугой окружности радиуса R. При этом дуга мало отличается от хорды АВ. Треугольники АОB и АСD подобны, как равнобедренные.
можно считать дугой окружности радиуса R. При этом дуга мало отличается от хорды АВ. Треугольники АОB и АСD подобны, как равнобедренные.
Отсюда следует, что
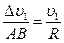 (1.15)
(1.15)
При 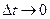 ,
,  , но так как
, но так как 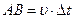 , то
, то
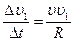 (1.16)
(1.16)
и получаем
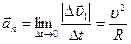 (1.17)
(1.17)
Нормальное ускорение 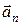 также называют центростремительным ускорением. Оно направлено по нормали к касательной к центру кривизны траектории.
также называют центростремительным ускорением. Оно направлено по нормали к касательной к центру кривизны траектории.
Полное ускорение есть геометрическая сумма тангенциальной и нормальной составляющих (рис. 1.5):
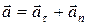 (1.18)
(1.18)
При 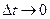 имеем
имеем 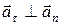 .
.
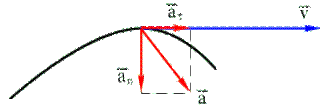
Рис. 1.5
В зависимости от 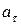 и
и 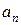 движение можно классифицировать следующим образом:
движение можно классифицировать следующим образом:
1. 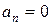 ,
, 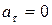 – движение прямолинейное равномерное;
– движение прямолинейное равномерное;
2. 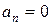 ,
, 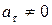 – движение прямолинейное ускоренное;
– движение прямолинейное ускоренное;
3. 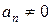 ,
,  ,
, 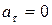 – равномерное движение по окружности.
– равномерное движение по окружности.
Движение по криволинейной траектории можно представить как прямолинейное движение и движение по окружностям разных радиусов (рис. 1.6)

Рис. 1.6
1.3. Движение материальной точки
по окружности
Если материальная точка движется по окружности, то ее движение иногда удобнее oписывать не линейными величинами S, 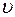 , a, а угловыми: углом поворота φ, угловой скоростью ω и угловым ускорением e.
, a, а угловыми: углом поворота φ, угловой скоростью ω и угловым ускорением e.
Рассмотрим движение точки по окружности радиуса R (рис. 1.7) Пусть через промежуток времени 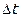 положение точки определяется углом поворота
положение точки определяется углом поворота  .
.
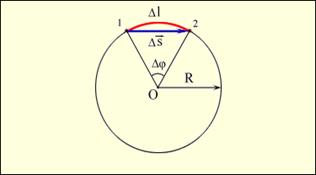
Рис. 1.7
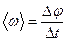 – средняя угловая скорость
– средняя угловая скорость
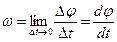 – мгновенная угловая скорость.
– мгновенная угловая скорость.
Угловая скорость – величина векторная. Модуль вектора угловой скорости равен значению угловой скорости ω, а его направление 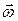 связано с осью вращения
связано с осью вращения 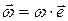 (где
(где 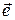 – единичный вектор вдоль оси вращения) и определяется по правилу правого винта: направление поступательного движения винта совпадает с направлением вектора угловой скорости (см. рис. 1.8).
– единичный вектор вдоль оси вращения) и определяется по правилу правого винта: направление поступательного движения винта совпадает с направлением вектора угловой скорости (см. рис. 1.8).
Размерность угловой скорости [ω] = рад/с, ([ω] = с-1).
Для малого угла Δφ установим связь между линейной и угловой скоростями.
 (1.19)
(1.19)
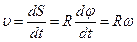 (1.20)
(1.20)
В векторной форме 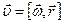

Рис. 1.8
При равномерном вращении ( 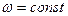 )
)
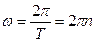
Τ – период вращения – время одного полного оборота точки,
n – частота вращения – количество оборотов в единицу времени; 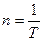
При неравномерном вращении ( 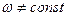 )
)
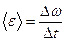 – среднее угловое ускорение
– среднее угловое ускорение
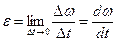
 – мгновенное угловое ускорение
– мгновенное угловое ускорение
Угловое ускорение – величина векторная 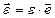 , где
, где 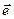 – единичный вектор, совпадающий с направлением оси вращения.
– единичный вектор, совпадающий с направлением оси вращения.
Если 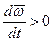 , вектор углового ускорения
, вектор углового ускорения 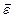 совпадает с направлением вектора угловой скорости
совпадает с направлением вектора угловой скорости 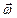 – вращение равноускоренное;
– вращение равноускоренное;
Если 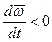 , вектор углового ускорения
, вектор углового ускорения 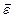 направлен противоположно вектору угловой скорости
направлен противоположно вектору угловой скорости 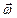 – вращение равнозамедленное.
– вращение равнозамедленное.
Размерность углового ускорения [e] = рад/с2, ([e]= с-2).
Установим связь между линейным и угловым ускорениями.
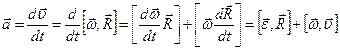
Так как 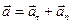 , то
, то 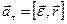 ,
, 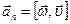 .
.
Законы движения точки (тела) по окружности аналогичны законам поступательного движения. Уравнение вращательного движения можно вывести из уравнений поступательного движения, заменив путь S углом поворота φ, скорость u – угловой скоростью ω, ускорение а – угловым ускорением ε.
Например,
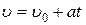 ®
® 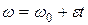
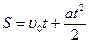 ®
® 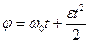
| <== предыдущая лекция | | | следующая лекция ==> |
| Тестомесильные машины непрерывного действия | | | Основы охраны труда. Правовые основы законодательства. |
Дата добавления: 2019-12-09; просмотров: 515;











