Понятия о переменных состояния.

Как правило, все ЭТУ являются или многомерными, или многоконтурными системами, то есть регулируются либо множеством выходных переменных, либо производными этих переменных для обеспечения заданного режима производственного процесса или предотвращения аварийных ситуаций.

Поведение даже одномерной системы описывается дифференциальным уравнением, производную каждого порядка этого дифференциального уравнения можно выделить в отдельную переменную, число которых равно порядку уравнения, повышенного порядка.

Число переменных состояния обязательно равно числу элементов системы, способных запасать существующую энергию.

Поведение линейной системы описывается однородным дифференциальным уравнением:

;

,

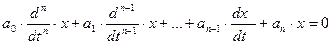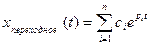но общее решение уравнения представляется в виде суммы:

X(t)=Хпер,(t)+Хуст(t) , где

Хуст(t)- частное решение неоднородного уравнения:

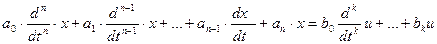
U- управляющее воздействие, а коэффициенты показывают степень эффективности влияния на объект каждой из производной этого воздействия.

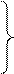Х=Х1

Х′=Х1′

Х1′=Х2

Х2=Х3

Если таким образом представить производные дифференциального уравнения, тогда, например, вместо дифференциального уравнения пятого порядка можно записать пять дифференциальных уравнений первого порядка, которые проще анализировать и реализовывать с помощью электронных и вычислительных устройств.

В общем случае динамические системы в переменных состояния описываются следующим образом:

Х′=АХ+ВU

у=СХ

И регулируемая величина, и управляющее воздействие имеют характеристики, зависящие от скорости и функционального характера их изменения во времени, так как каждая производная относится к определенному элементу, запасающему энергию, и поэтому всегда существуют режимы управления, оптимальные с точки зрения определенных критериев:

- минимум расхода энергии;

- минимум времени достижения заданного значения;

- заданный закон изменения во времени регулируемой величины, включая перерегулирования.